В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie "High-frequency market-making with inventory constraints and directional bets" . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них не учитывается действие adverse selection risk . Поэтому в данной части рассмотрим работу JIANGMIN XU "Optimal Strategies of High Frequency Traders", в которой автор делает попытку учесть этот вид риска.
Для этого необходимо получить предсказание направления движения цены в коротком промежутке времени ( мы говорим о высокочастотных алгоритмах, поэтому такой промежуток будет измеряться в секундах, или даже долях секунды). JIANGMIN XU предлагает учитывать зависимость цены от дисбаланса объемов в стакане, который равен разности между логарифмами объема лучшей покупки и объема лучшей продажи 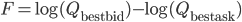 . Этот дисбаланс следует процессу Орнштейна-Уленбека с нулевым средним:
. Этот дисбаланс следует процессу Орнштейна-Уленбека с нулевым средним:
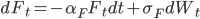 , где
, где
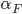 - константа, отражающая скорость колебаний вокруг среднего,
- константа, отражающая скорость колебаний вокруг среднего,
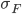 - постоянная, отражающая волатильность процесса,
- постоянная, отражающая волатильность процесса,
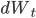 - случайный броуновский процесс.
- случайный броуновский процесс.
Далее нам понадобится модель спреда 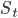 - разницы цен между лучшим аском и лучшим бидом- которая представляет собой марковский процесс с тремя состояниями -
- разницы цен между лучшим аском и лучшим бидом- которая представляет собой марковский процесс с тремя состояниями - 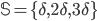 , где
, где 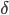 - шаг цены. Матрицу вероятностей переходов обозначим
- шаг цены. Матрицу вероятностей переходов обозначим 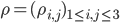 ,
, 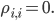
В качестве модели прироста цены актива возьмем один из видов марковского процесса - pure-jump process :
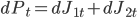 , где
, где
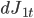 - первая составляющая имеет интенсивность скачков цены
- первая составляющая имеет интенсивность скачков цены 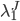 , величину скачка
, величину скачка 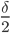 с вероятностью
с вероятностью 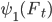 и величину скачка
и величину скачка 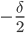 с вероятностью
с вероятностью 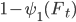 ,
,
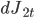 - вторая составляющая имеет интенсивность скачков
- вторая составляющая имеет интенсивность скачков 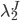 , величину скачка
, величину скачка 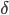 с вероятностью
с вероятностью 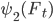 и величину скачка
и величину скачка 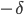 с вероятностью
с вероятностью 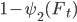 ,
,
где функция 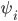 имеет форму
имеет форму
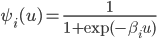 , для i =1,2.
, для i =1,2.
Дисбаланс объемов 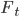 в стакане влияет на скачок цены в следующий момент времени таким образом: если
в стакане влияет на скачок цены в следующий момент времени таким образом: если 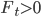 цена с большей вероятностью будет расти и наоборот. Этот сигнал конечно не идеален, но позволяет предсказывать цену на каком-то временном промежутке и будет полезен для формирования формулы оптимального управления рисками в рамках HFT стратегии.
цена с большей вероятностью будет расти и наоборот. Этот сигнал конечно не идеален, но позволяет предсказывать цену на каком-то временном промежутке и будет полезен для формирования формулы оптимального управления рисками в рамках HFT стратегии.
Сформулируем основные стратегии для HFT алгоритма:
1. Котирование (make strategy). В рамках этой стратегии алгоритм может располагать лимитные ордера на best bid или best ask, а если спред 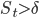 , то ордера могут располагаться на ценовых уровнях
, то ордера могут располагаться на ценовых уровнях 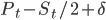 (
(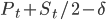 ), для увеличения вероятности взятия ордера с меньшими затратами,чем затраты при гарантированном исполнении (если, конечно, не учитывать задержки выставления) маркет ордера. Эту модель представим в виде непрерывного процесса:
), для увеличения вероятности взятия ордера с меньшими затратами,чем затраты при гарантированном исполнении (если, конечно, не учитывать задержки выставления) маркет ордера. Эту модель представим в виде непрерывного процесса:
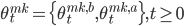 , где
, где
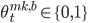 и
и 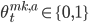 . b и a означают bid и ask соответственно. Таким образом 0 означает постановку ордера на лучшую цену покупки или продажи, а 1 означает постановку ордера на лучшую цену плюс/минус
. b и a означают bid и ask соответственно. Таким образом 0 означает постановку ордера на лучшую цену покупки или продажи, а 1 означает постановку ордера на лучшую цену плюс/минус 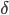 . Если спред минимальный -
. Если спред минимальный - 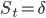 то значение
то значение 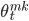 может быть равно только 0.
может быть равно только 0.
2. Использование маркет ордеров (take strategy). Для получения мгновенного исполнения алгоритм может использовать маркет ордера. Маркет ордер, в отличие от лимитного, забирает ликвидность из стакана и имеет высокую стоимость, равную половине спреда (без учета комиссии). Смоделируем данную стратегию как импульсный процесс в непрерывном времени:
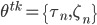 , где
, где
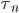 - возрастающая последовательность моментов времени, когда используется маркет ордер,
- возрастающая последовательность моментов времени, когда используется маркет ордер,
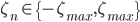 - случайная переменная, представляющая число контрактов, купленных или проданных в эти моменты времени.
- случайная переменная, представляющая число контрактов, купленных или проданных в эти моменты времени.
Для чего нужны все вышеописанные модели? Наша цель - составить уравнение оптимального контроля, в котором будет учтен как inventory risk, так и adverse selection risk. А решением этого уравнения будет матрица состояний, которую можно представить в виде графика с двумя осями значений - первая ось inventory level, это текущая открытая позиция, вторая ось - depth imbalance, то есть дизбаланс объемов в стакане. Таким образом эти оси значений представляют собой аргументы по которым происходит управление - по первой оси - inventory risk, по второй оси - adverse selection risk. Матрица состояний представляет собой множество значений 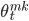 и
и 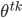 . Их можно представить на графике в виде области внутри квадрата, ограниченного рассмотренными осями значений. Такой график представлен в заглавии поста, для значения спреда
. Их можно представить на графике в виде области внутри квадрата, ограниченного рассмотренными осями значений. Такой график представлен в заглавии поста, для значения спреда 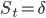 , на момент времени t=10 (за единицу времени может быть принят любой интервал, в зависимости от требуемой частоты сделок). На графике выделены следующие области:
, на момент времени t=10 (за единицу времени может быть принят любой интервал, в зависимости от требуемой частоты сделок). На графике выделены следующие области:
1. Market making - в этой области выставляются ордера как на покупку так и на продажу по ценам best bid и best ask, то есть 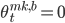 и
и 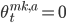 ;
;
2. Momentum (buy/sell). В этих областях необходимо срочное закрытие позиций, если они открыты в сторону, противоположную дизбалансу объемов и установление позиции согласно этому дизбалансу. Здесь используются маркет ордера, и 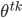 равен какому-то количеству контрактов, больше открытой позиции по модулю, противоположному по знаку.Точная величина зависит от значений на осях аргументов.
равен какому-то количеству контрактов, больше открытой позиции по модулю, противоположному по знаку.Точная величина зависит от значений на осях аргументов.
3. Inventory control (buy/sell). Эти области означают ликвидацию открытых позиций в ноль, также с использованием маркет ордеров, 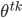 равен открытой позиции с противоположным знаком.
равен открытой позиции с противоположным знаком.
4. Partial inventory control (buy/sell). Эти области аналогичны inventory control, но открытая позиция закрывается не полностью, 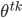 меньше открытой позиции по модулю,противоположна по знаку. Точная величина зависит от значений на осях аргументов.
меньше открытой позиции по модулю,противоположна по знаку. Точная величина зависит от значений на осях аргументов.
В следующих статьях мы составим уравнение оптимального контроля и найдем его решение численными методами.


 (3 голосов, средний: 3,67 из 5)
(3 голосов, средний: 3,67 из 5)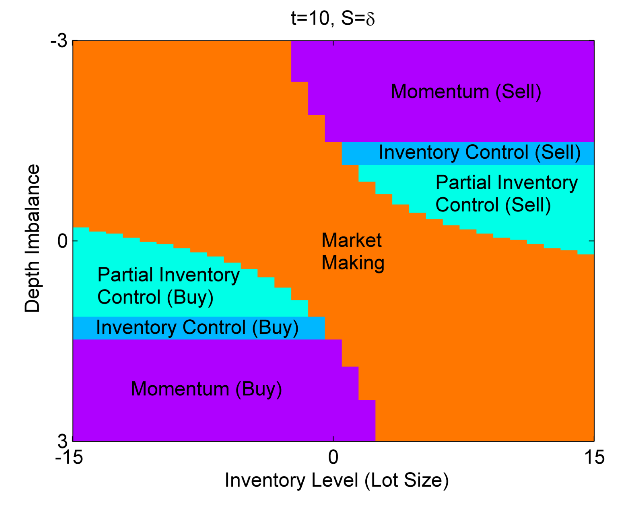


Вы проверяли достоверность гипотезы о влиянии дисбаланса объемов на направление движения цены на реальных данных?
Да, проверял. Зависимость имеет место быть, правда на очень коротких промежутках времени. Но вам ничто не мешает использовать и другие сигналы в этом алгоритме. Правда, должно соблюдаться условие о следованию процессу Орнштейна-Уленбека
Проверяю на данных российского рынка.
Данные: ордерлог + лимитные заявки (стакан) фьючерса Si 06.15.
Выборка содержит 220,736 наблюдений.
Временной интервал с 10:05 до 16:00.
1. Гипотеза о следовании дисбаланса объмов процессу Орнштейна-Уленбека с нулевым средним достоверна. Процесс стационарный dFt=-0.1608765*Ft*dt+1.0266176*dWt
2. В качестве интервала предсказаний я выбрал все-таки количество тиков, а не время. Временной интервал предсказаний можно оценить по интенсивности сделок в секунду:
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 3.00 8.00 12.74 17.00 355.00
3. Для повышений точности предсказаний и наглядности результатов установлены пороговые значения дисбаланса: абсолютное значение дисбаланса больше 100 контрактов.
4. Результаты следующие:
Видно, что на совсем коротких интервалах точность предсказания низкая. Потом происходит увеличени до некоторого максимального значения. Далее точность уменьшается.
Конечно данные необходимо перепроверять на разных выборках.
Очень интересное исследование, спасибо. Я сам так не находил времени сделать. Только смутило значение порога в 100 контрактов: в моих статьях идет речь о разнице объемов на лучшем биде и аске - а на них разве часто будет превышен такой порог?
А, не заметил, что речь идет о Si. Я все расчеты производил на данных фьючерса RI
Выбрал для анализа Si как наиоболее ликвидный интрумент на нашей срочке. Конкретно на это выборке порог превышался около 5-6 тыс раз по каждой стороне. То есть вполне можно торговать. Еще на Si спреды бид/аск прыгают постоянно. Среднее значение 5 рублей по выборке. Что скорее является плюсом для Вашего алгоритма. Такое впечталение, что маркетмэйкер на Si не очень активен.
Приложу еще картинку анимацию для разных значений порогов
<a href="http://tinypic.com?ref=hvcqxt" target="_blank"><img src="http://i57.tinypic.com/hvcqxt.gif" border="0" alt=""></a>
Если возможно, подскажите, пожалуйста, как по имевшимся данным были оценены параметры приведенного уравнения для процесса Орнштейна-Уленбека.
В части пятой про алгоритм маркетмейкера указан метод оценки этих параметров, дана формула для их нахождения методом максимального правдоподобия
Большое спасибо, просто в статье-первоисточнике не смог найти.
r0man, как Вы оценивали параметры процесса Орнштейна-Уленбека ? Так же как uralpro в 5-ой части?