В этой, последней части цикла разберем пример вычисления PIN с применением языка R. Кроме библиотеки PIN языка R будем использовать также библиотеку highfrequency.
Для примера автор берет сгенерированные данные, которые соответствуют формату TAQ - стандарт для акций NYSE. Данные состоят из двух наборов - временной ряд ценового котирования (sample_qdata) и сделки (sample_tdata) и предоставляются в открытом доступе вместе с библиотекой highfrequency.
Нужно отметить что используемые данные взяты только за один торговый день. Обычно, для вычисления PIN применяют больший набор данных, не менее, чем за 60 дней, чтобы выборка была достаточной для правильного определения параметров. Наши данные нужны только для демонстрации процесса получения PIN. Библиотека PIN позволяет это сделать для выборки с любой размерностью, что позволяет применять ее и для высокочастотной торговли. Пример, приводимый здесь, может быть легко расширен для вычисления на другом временном горизонте, большим, чем один торговый день.
В начале загрузим все необходимые библиотеки R:
library(zoo) library(xts) library(highfrequency) library(TTR) library(timeDate) library(quantmod) library(PIN)
Затем, подготовим набор данных для вычисления PIN. Так как у нас есть два временных ряда - квоты и сделки, их нужно совместить и слить в один ряд для данного торгового дня:
#загружаем примеры data(sample_tdata) data(sample_qdata) #Совмещаем данные tqdata <- matchTradesQuotes(sample_tdata, sample_qdata)
Данные, используемые для примера, не содержат информации о направлении сделок. Это может иметь место на некоторых рынках ( но не на российских биржах), и для классификации сделок можно применить соотвествующие алгоритмы, предлагаемые в финансовой литературе. В данном случае автор использует подход Lee-Ready, который включен в библиотеку highfrequency:
x <- getTradeDirection(tqdata) tradeDirection <- matrix(x) buy_side <- which(tradeDirection > 0) num_buy_side <- length(matrix(buy_side)) num_sell_side <- length(tradeDirection) - length(matrix(buy_side)) ntrades <- cbind(num_buy_side, num_sell_side)
Максимизация функции вероятности, рассмотренной нами в части 2, предваряет вычисление PIN. В идеальном случае необходимо произвести оптимизацию, ограничивающую значение всех параметров интервалом [0,1]. Для нашего случая применим общую функцию оптимизации optim:
initparams <- cbind(0.15, 0.05, 0.5, 0.5) options(warn = -1) param_optim <- optim(initparams, pin_likelihood, gr = NULL, ntrades)
Выражение для функции вероятности содержится в pin_likelihood. В первой строчке задаются начальные значения параметров.
У нас получились следующие значения оптимизированных параметров ϵ,μ,α,δ - 1, 0.3715623, 0.7255069 и 0.2808594 соответственно. Эти параметры означают, что в данный день наличествует высокая вероятность прихода новостей ( α=0.72). Если новостей не будет, только неинформированные трейдеры примут участие в торгах (ϵ=1).
В окончании, получив оптимизированные параметры, легко вычисляем вероятность информированной торговли:
epsi <- param_optim$par[1] miu <- param_optim$par[2] alph <- param_optim$par[3] delt <- param_optim$par[4] pin <- (alph*miu)/(alph*miu + 2*epsi)
В данном примере, мы констатируем низкую вероятность торговли с информированным контрагентом, которая равна 0.1187762.
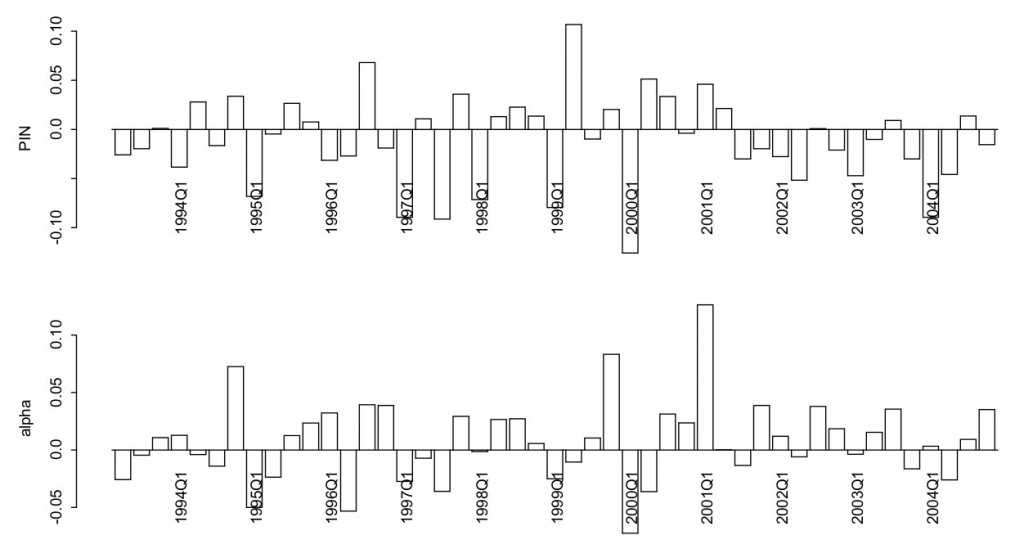
В заглавии поста приведена гистограмма значений PIN и верятности прихода новостей α для каждого квартала с 1994 по 2004 год для биржи NYSE. Прошу обратить внимание, что невысокие значения PIN обусловлены тем, что они вычислены на этом графике за целый квартал, поэтому размерность величины значительно отличается от нашего примера, где мы находим дневной PIN ( для одного дня значение 0.1 трактуется как небольшое, для квартала это же значение может означать большую вероятность присутствия информированных трейдеров).
Применение рассмотренной нами вероятности информированной торговли PIN может быть расширено в нескольких направлениях. Возможно добавление альтернативных измерителей ассиметричности торговли, например, динамический PIN, представленный в этой работе. Также, ставшая де-факто стандартом финансовой индустрии, синхронизированная по объемам вероятность информированной торговли VPIN, которая будет предметом рассмотрения в будущих статьях.
Предоставление ликвидости на рынке зависит от присутствия ассиметричной информации. Измерение этой ассиметричности особенно необходимо маркет мейкерам, которые управляют своими активами, и подвержены adverse selection risk, то есть риску того, что контрагенты в сделках обладают более полной информацией о цене актива. Таким образом, вычисление PIN улучшает видение рынка при отсутствии других данных о ликвидности.
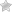


Инструмент полезный. Сложность пожалуй будет составлять численная максимизация функции вероятности, если делать в других языках.