В прошлой части мы продемонстрировали обучение модели Маркова на данных, полученных с помощью симуляции. В данной статье рассмотрим производительность модели на реальных данных. Будем тестировать трендследящую стратегию на индексе S&P500.
В большинстве задач с использованием машинного обучения требуются обучающие данные с разметкой классов (состояний). В нашем случае такой разметки нет, поэтому сначала сгенерируем классы для обучающей выборки.
Мы хотим создать трендследящую стратегию, поэтому должны выбрать участки на выборке цен S&P500, которые соответствуют восходящему и нисходящему трендам ( также можно отметить участки, где тренды отсутствуют). Можно это сделать вручную, а можно применить программу, которая автоматически расставит метки в соответствии с вашими определениями тренда.
На графике внизу показана разметка, где красная метка над графиком цены обозначает нисходящий тренд, зеленая метка под графиком - восходящий.
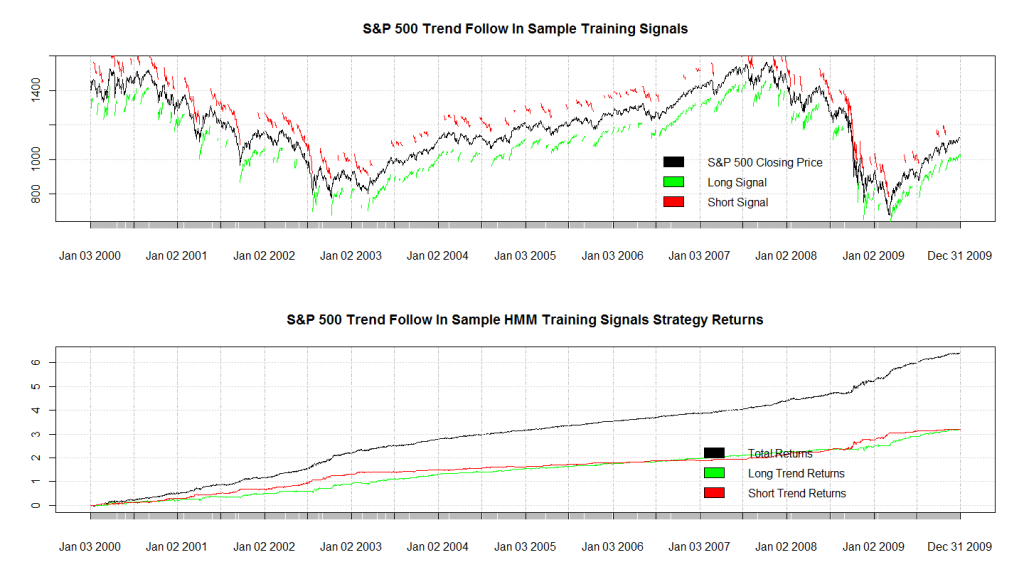 В коде, который будет приведен ниже определение трендов происходит следующим образом: если текущая цена самая низкая из цен 10 последующих периодов то отмечается начало восходящего тренда, до момента, когда текущая цена становится самой высокой для последующих 10 периодов, после которых тренд закрывается. Для нисходящего тренда все с точностью до наоборот. Это несколько грубое определение, и наверняка есть более точная методика определения трендов, которая учитывает волатильность цен, думаю,ее вы можете разработать сами.
В коде, который будет приведен ниже определение трендов происходит следующим образом: если текущая цена самая низкая из цен 10 последующих периодов то отмечается начало восходящего тренда, до момента, когда текущая цена становится самой высокой для последующих 10 периодов, после которых тренд закрывается. Для нисходящего тренда все с точностью до наоборот. Это несколько грубое определение, и наверняка есть более точная методика определения трендов, которая учитывает волатильность цен, думаю,ее вы можете разработать сами.
В дополнение к разметке, необходимо сгенерировать вектор параметров, нужных для определения тренда. Для этого мы использовали индикаторы, представляющие собой отношения цены открытия к цене закрытия, цены открытия к минимальной цене, цены открытия к максимальной цене и другие возможные отношения для каждого периода. В большинстве случаев желательно включить в вектор параметров динамику изменения этих индикаторов, хотя бы за 1 период.
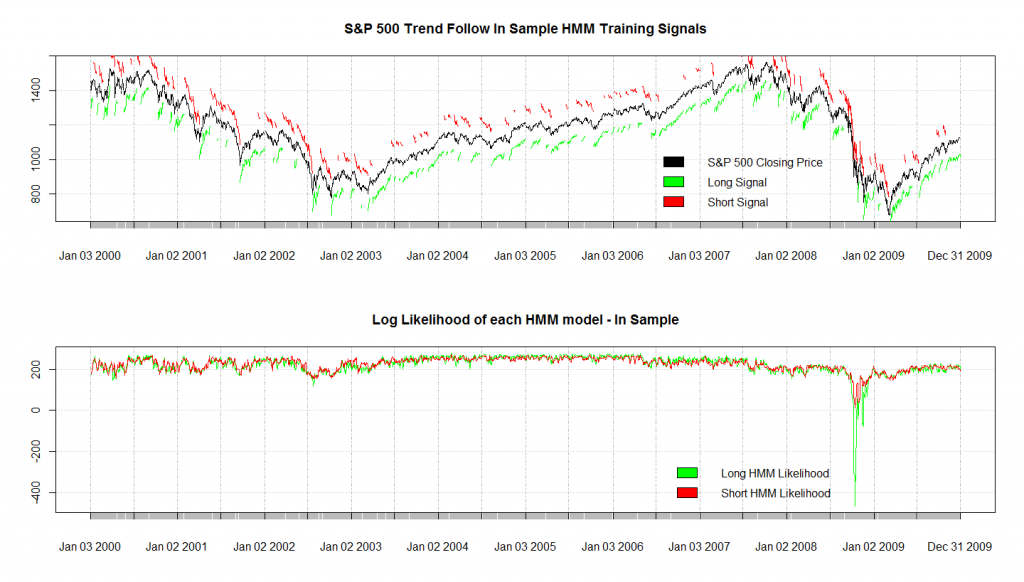 На графике выше показана вероятность каждого режима ( тренда) , полученную с помощью модели Маркова, обученной на тех же данных. Видно, что вход в длинную позицию был крайне нежелателен прямо перед и во время обвала 2008 года.
На графике выше показана вероятность каждого режима ( тренда) , полученную с помощью модели Маркова, обученной на тех же данных. Видно, что вход в длинную позицию был крайне нежелателен прямо перед и во время обвала 2008 года.
Одним из замечательных свойств модели Маркова является то, что она позволяет распознать ситуации, когда существует один и тот же класс (состояние), но его продолжительность в каждой ситуации сильно различается . Например, в одном случае тренд длится 10 дней, в другом - 35 дней, мы можем оба примера пропустить через модель , и в результате получим правильное распознавание через использование внутренних вероятностей перехода состояний модели.
В заголовке поста показаны результаты тестирования модели на проверочной выборке (out-of-sample). На третьем графике черной линией показана общая прибыльность алгоритма, зеленой линией - прибыльность при входе только в длинную позицию, красной - только в короткую. Можно сделать вывод о хорошей производительности стратегии распознавания трендов с помощью модели Маркова.
Полученные параметры модели Маркова : для восходящего тренда
HMMFit(obs = inSampleLongFeaturesList, nStates = 3)
Model:
------
3 states HMM with 7-d gaussian distribution
Baum-Welch algorithm status:
----------------------------
Number of iterations : 21
Last relative variation of LLH function: 0.000001
Estimation:
-----------
Initial probabilities:
Pi 1 Pi 2 Pi 3
1.690213e-47 0.3734194 0.6265806
Transition matrix:
State 1 State 2 State 3
State 1 0.4126480 0.3419075 0.24544450
State 2 0.1116068 0.8352273 0.05316591
State 3 0.5475525 0.2303324 0.22211504
Conditionnal distribution parameters:
Distribution parameters:
State 1
mean cov matrix
0.01565943 1.922717e-04 1.724953e-04 1.785035e-04 -7.870798e-06 -1.764319e-04 -1.687845e-04 6.898374e-06
1.02210441 1.724953e-04 1.920546e-04 1.736241e-04 2.327852e-06 -1.615346e-04 -1.768012e-04 -1.651055e-05
1.01805768 1.785035e-04 1.736241e-04 1.777602e-04 2.663971e-06 -1.653924e-04 -1.595871e-04 5.067094e-06
1.00264545 -7.870798e-06 2.327852e-06 2.663971e-06 1.095711e-05 8.195588e-06 8.473222e-06 3.178401e-07
0.98502360 -1.764319e-04 -1.615346e-04 -1.653924e-04 8.195588e-06 1.644647e-04 1.589815e-04 -4.749521e-06
0.98113485 -1.687845e-04 -1.768012e-04 -1.595871e-04 8.473222e-06 1.589815e-04 1.732240e-04 1.542815e-05
0.99605695 6.898374e-06 -1.651055e-05 5.067094e-06 3.178401e-07 -4.749521e-06 1.542815e-05 2.064964e-05
State 2
mean cov matrix
0.001670502 3.103878e-05 3.555352e-06 1.781044e-05 -1.336108e-05 -3.092612e-05 -1.670114e-05 1.410578e-05
1.009361131 3.555352e-06 1.249497e-05 9.181451e-06 5.644685e-06 -3.464184e-06 -6.714792e-06 -3.238512e-06
1.005638565 1.781044e-05 9.181451e-06 1.714606e-05 -7.256446e-07 -1.770669e-05 -9.748050e-06 7.905439e-06
1.003957940 -1.336108e-05 5.644685e-06 -7.256446e-07 1.271107e-05 1.335557e-05 7.009564e-06 -6.279198e-06
0.998346405 -3.092612e-05 -3.464184e-06 -1.770669e-05 1.335557e-05 3.081873e-05 1.660615e-05 -1.409313e-05
0.994653572 -1.670114e-05 -6.714792e-06 -9.748050e-06 7.009564e-06 1.660615e-05 1.353501e-05 -3.017033e-06
0.996315167 1.410578e-05 -3.238512e-06 7.905439e-06 -6.279198e-06 -1.409313e-05 -3.017033e-06 1.101157e-05
State 3
mean cov matrix
-0.01296153 1.481273e-04 -8.848326e-05 2.231101e-05 -1.286390e-04 -1.503760e-04 -3.945685e-05 1.032046e-04
1.02416584 -8.848326e-05 1.349494e-04 2.353928e-05 1.150009e-04 9.081677e-05 -1.853468e-05 -1.027771e-04
1.00458706 2.231101e-05 2.353928e-05 3.596043e-05 1.384302e-05 -2.234068e-05 -9.215909e-06 1.259424e-05
1.01746162 -1.286390e-04 1.150009e-04 1.384302e-05 1.485395e-04 1.338477e-04 3.324363e-05 -9.313984e-05
1.01283801 -1.503760e-04 9.081677e-05 -2.234068e-05 1.338477e-04 1.555764e-04 4.225851e-05 -1.053565e-04
0.99347206 -3.945685e-05 -1.853468e-05 -9.215909e-06 3.324363e-05 4.225851e-05 5.013390e-05 8.770049e-06
0.98098355 1.032046e-04 -1.027771e-04 1.259424e-05 -9.313984e-05 -1.053565e-04 8.770049e-06 1.075952e-04
Log-likelihood: 64226.28
BIC criterium: -127633.2
AIC criterium: -128226.6
для нисходящего тренда:
Short Model
HMMFit(obs = inSampleShortFeaturesList, nStates = 3)
Model:
------
3 states HMM with 7-d gaussian distribution
Baum-Welch algorithm status:
----------------------------
Number of iterations : 20
Last relative variation of LLH function: 0.000001
Estimation:
-----------
Initial probabilities:
Pi 1 Pi 2 Pi 3
3.784166e-15 0.1476967 0.8523033
Transition matrix:
State 1 State 2 State 3
State 1 0.4760408 0.12434214 0.3996170
State 2 0.3068272 0.54976794 0.1434049
State 3 0.5243733 0.06315371 0.4124730
Conditionnal distribution parameters:
Distribution parameters:
State 1
mean cov matrix
-0.009827328 5.102050e-05 -2.137629e-05 1.047989e-05 -3.999886e-05 -5.043558e-05 -1.834830e-05 3.090145e-05
1.016726031 -2.137629e-05 2.915402e-05 4.001168e-06 2.551672e-05 2.145395e-05 -3.484775e-06 -2.426317e-05
1.002951135 1.047989e-05 4.001168e-06 1.070077e-05 4.343448e-07 -1.032399e-05 -3.489498e-06 6.607115e-06
1.012808350 -3.999886e-05 2.551672e-05 4.343448e-07 4.073945e-05 4.019962e-05 1.502427e-05 -2.422162e-05
1.009838504 -5.043558e-05 2.145395e-05 -1.032399e-05 4.019962e-05 5.047663e-05 1.847048e-05 -3.082551e-05
0.996150195 -1.834830e-05 -3.484775e-06 -3.489498e-06 1.502427e-05 1.847048e-05 1.816514e-05 -3.045290e-08
0.986475577 3.090145e-05 -2.426317e-05 6.607115e-06 -2.422162e-05 -3.082551e-05 -3.045290e-08 2.992073e-05
State 2
mean cov matrix
-0.005393441 0.0008501205 -1.231927e-04 3.413652e-04 -0.0004927836 -0.0008165848 -3.496732e-04 4.379093e-04
1.037824136 -0.0001231927 3.546602e-04 7.820615e-05 0.0002160609 0.0001422901 -1.206772e-04 -2.508658e-04
1.013889133 0.0003413652 7.820615e-05 2.198099e-04 -0.0001068837 -0.0003166324 -1.713360e-04 1.374691e-04
1.019557602 -0.0004927836 2.160609e-04 -1.068837e-04 0.0003949026 0.0004952245 1.733093e-04 -2.998924e-04
1.005903113 -0.0008165848 1.422901e-04 -3.166324e-04 0.0004952245 0.0007960268 3.345499e-04 -4.319633e-04
0.982515481 -0.0003496732 -1.206772e-04 -1.713360e-04 0.0001733093 0.0003345499 2.726893e-04 -5.242376e-05
0.977179046 0.0004379093 -2.508658e-04 1.374691e-04 -0.0002998924 -0.0004319633 -5.242376e-05 3.611514e-04
State 3
mean cov matrix
0.003909801 2.934983e-05 1.656072e-05 2.335206e-05 -5.814278e-06 -2.877715e-05 -2.196575e-05 6.761736e-06
1.010126341 1.656072e-05 1.900251e-05 1.943331e-05 2.909245e-06 -1.625496e-05 -1.574899e-05 4.694645e-07
1.007300746 2.335206e-05 1.943331e-05 2.554298e-05 2.309188e-06 -2.288733e-05 -1.676155e-05 6.090567e-06
1.003413014 -5.814278e-06 2.909245e-06 2.309188e-06 8.147512e-06 5.796633e-06 5.191743e-06 -5.902698e-07
0.996163167 -2.877715e-05 -1.625496e-05 -2.288733e-05 5.796633e-06 2.830213e-05 2.164898e-05 -6.603805e-06
0.993369564 -2.196575e-05 -1.574899e-05 -1.676155e-05 5.191743e-06 2.164898e-05 2.055797e-05 -1.040800e-06
0.997202266 6.761736e-06 4.694645e-07 6.090567e-06 -5.902698e-07 -6.603805e-06 -1.040800e-06 5.564118e-06
Log-likelihood: 47728.08
BIC criterium: -94666.79
AIC criterium: -95230.16
Код для обучения и применения модели Маркова на языке R:
library("quantmod")
library("PerformanceAnalytics")
library('RHmm') #Load HMM package
library('zoo')
#Выбираем даты для загружаемых данных
startDate = as.Date("2000-01-01") #Начальная дата
trainingEndDate = as.Date("2010-01-01") # Начальная дата для обучающей выборки
NDayLookforwardLowHigh < - 10 # Параметр, используемый для классификации тренда
HmmLikelihoodTestLength <- 5 # сколько периодов данных нужно для вычисления отношения вероятностей для сравнения моделей
symbolData <- new.env() #Make a new environment for quantmod to store data in
symbol <- "^GSPC" #S&p 500
getSymbols(symbol, env = symbolData, src = "yahoo", from = startDate)
mktdata <- eval(parse(text=paste("symbolData$",sub("^","",symbol,fixed=TRUE))))
mktdata <- head(mktdata,-1) #Hack to fix some stupid duplicate date problem with yahoo
inSampleMktData <- window(mktdata,start=startDate ,end=trainingEndDate)
outOfSampleMktData <- window(mktdata,start=trainingEndDate+1)
dailyRet <- Delt(Cl(mktdata),k=1,type="arithmetic") #Daily Returns
dailyRet[is.na(dailyRet)] <-0.00001
inSampleDailyRet <- window(dailyRet,start=startDate ,end=trainingEndDate)
outOfSampleDailyRet <- window(dailyRet,start=trainingEndDate+1)
ConvertTofullSignal <- function(signal){
results <- rep(0,length(signal))
intrade <- F
for(i in seq(1,length(signal))){
if(signal[i]==-1){
intrade <- F
}
if(signal[i]==1 || intrade){
results[i]<-1
intrade <- T
}
}
return(results)
}
#Генерируем сигнал для восходящего тренда
LongTrendSignal <- rep(0,nrow(inSampleMktData))
for(i in seq(1,nrow(inSampleMktData)-NDayLookforwardLowHigh)){
dataBlock <- Cl(inSampleMktData[seq(i,i+NDayLookforwardLowHigh),])
if(coredata(Cl(inSampleMktData[i,])) == min(coredata(dataBlock))){
LongTrendSignal[i] <- 1
}
if(coredata(Cl(inSampleMktData[i,])) == max(coredata(dataBlock))){
LongTrendSignal[i] <- -1
}
}
LongTrendSignal <- ConvertTofullSignal(LongTrendSignal)
#Генерируем сигнал для нисходящего тренда
ShortTrendSignal <- rep(0,nrow(inSampleMktData))
for(i in seq(1,nrow(inSampleMktData)-NDayLookforwardLowHigh)){
dataBlock <- Cl(inSampleMktData[seq(i,i+NDayLookforwardLowHigh),])
if(coredata(Cl(inSampleMktData[i,])) == max(coredata(dataBlock))){
ShortTrendSignal[i] <- 1
}
if(coredata(Cl(inSampleMktData[i,])) == min(coredata(dataBlock))){
ShortTrendSignal[i] <- -1
}
}
ShortTrendSignal <- ConvertTofullSignal(ShortTrendSignal)
#Рисуем полученные сигналы
LongTrendSignalForPlot <- LongTrendSignal
LongTrendSignalForPlot[LongTrendSignalForPlot==0] <- NaN
LongTrendSignalForPlot <- Cl(inSampleMktData)*LongTrendSignalForPlot - 100
inSampleLongTrendSignalForPlot <-LongTrendSignalForPlot
ShortTrendSignalForPlot <- ShortTrendSignal
ShortTrendSignalForPlot[ShortTrendSignalForPlot==0] <- NaN
ShortTrendSignalForPlot <- Cl(inSampleMktData)*ShortTrendSignalForPlot + 100
inSampleShortTrendSignalForPlot <- ShortTrendSignalForPlot
dev.new()
layout(1:2)
plot(Cl(inSampleMktData), main="S&P 500 Trend Follow In Sample Training Signals")
lines(inSampleLongTrendSignalForPlot,col="green",type="l")
lines(inSampleShortTrendSignalForPlot,col="red",type="l")
legend(x='bottomright', c("S&P 500 Closing Price","Long Signal","Short Signal"), fill=c("black","green","red"), bty='n')
#Вычисляем прибыльность
LongReturns <- Lag(LongTrendSignal)* (inSampleDailyRet)
LongReturns[is.na(LongReturns)] <- 0
ShortReturns <- Lag(-1*ShortTrendSignal)* (inSampleDailyRet)
ShortReturns[is.na(ShortReturns)] <- 0
TotalReturns <- LongReturns + ShortReturns
plot(cumsum(TotalReturns),main="S&P 500 Trend Follow In Sample HMM Training Signals Strategy Returns")
lines(cumsum(LongReturns),col="green")
lines(cumsum(ShortReturns),col="red")
legend(x='bottomright', c("Total Returns","Long Trend Returns","Short Trend Returns"), fill=c("black","green","red"), bty='n')
#Загружаем список параметров для каждого класса
CreateListOfMatrixFeatures <- function(features,signal){
results <- list()
extract <- F
for(i in seq(1,length(signal))){
if(signal[i]==1 && !extract){
startIndex <- i
extract <- T
}
if(signal[i]==0 && extract){
endIndex <- i-1
dataBlock <- features[startIndex:endIndex,]
extract <- F
#print(dataBlock)
results[[length(results)+1]] <- as.matrix(dataBlock)
}
}
return(results)
}
#Тренировка модели
#Генерируем параметры, описывающие данные и разделяем выборку на обучающую и проверочную
features <- cbind(dailyRet,Hi(mktdata)/Lo(mktdata),Hi(mktdata)/Op(mktdata),Hi(mktdata)/Cl(mktdata),Op(mktdata)/Cl(mktdata),Lo(mktdata)/Cl(mktdata),Lo(mktdata)/Op(mktdata))
inSampleTrainingFeatures <- window(features,start=startDate ,end=trainingEndDate)
outOfSampleFeatures <- window(features,start=trainingEndDate+1)
#Для каждого вида тренда получаем соответствующие параметры и создаем их вектор
inSampleLongFeaturesList <- CreateListOfMatrixFeatures(inSampleTrainingFeatures,LongTrendSignal)
inSampleShortFeaturesList <- CreateListOfMatrixFeatures(inSampleTrainingFeatures,ShortTrendSignal)
#Тренируем модель
LongModelFit = HMMFit(inSampleLongFeaturesList, nStates=3)
ShortModelFit = HMMFit(inSampleShortFeaturesList, nStates=3)
#Берем NDayLookforwardLowHigh периодов данных и вычисляем скользящий логарифм вероятности для каждой модели
inSampleLongLikelihood <- rollapply(inSampleTrainingFeatures,HmmLikelihoodTestLength,align="right",na.pad=T,by.column=F,function(x) {forwardBackward(LongModelFit,as.matrix(x))$LLH})
inSampleShortLikelihood <- rollapply(inSampleTrainingFeatures,HmmLikelihoodTestLength,align="right",na.pad=T,by.column=F,function(x) {forwardBackward(ShortModelFit,as.matrix(x))$LLH})
outOfSampleLongLikelihood <- rollapply(outOfSampleFeatures,HmmLikelihoodTestLength,align="right",na.pad=T,by.column=F,function(x) {forwardBackward(LongModelFit,as.matrix(x))$LLH})
outOfSampleShortLikelihood <- rollapply(outOfSampleFeatures,HmmLikelihoodTestLength,align="right",na.pad=T,by.column=F,function(x) {forwardBackward(ShortModelFit,as.matrix(x))$LLH})
#Создаем сигналы для графика/торговли
outOfSampleLongTrendSignalForPlot <- 1*(outOfSampleLongLikelihood > outOfSampleShortLikelihood)
outOfSampleLongTrendSignalForPlot[outOfSampleLongTrendSignalForPlot==0] < - NaN
outOfSampleLongTrendSignalForPlot <- outOfSampleLongTrendSignalForPlot*Cl(outOfSampleMktData)-100
outOfSampleShortTrendSignalForPlot <- 1*(outOfSampleLongLikelihood < outOfSampleShortLikelihood)
outOfSampleShortTrendSignalForPlot[outOfSampleShortTrendSignalForPlot==0]<-NaN
outOfSampleShortTrendSignalForPlot <- outOfSampleShortTrendSignalForPlot*Cl(outOfSampleMktData)+100
dev.new()
layout(1:2)
plot(Cl(inSampleMktData), main="S&P 500 Trend Follow In Sample HMM Training Signals")
lines(inSampleLongTrendSignalForPlot,col="green",type="l")
lines(inSampleShortTrendSignalForPlot,col="red",type="l")
legend(x='bottomright', c("S&P 500 Closing Price","Long Signal","Short Signal"), fill=c("black","green","red"), bty='n')
#tt <- Cl(inSampleMktData)
#tt[,1] <- inSampleLongLikelihood
plot(inSampleLongLikelihood,main="Log Likelihood of each HMM model - In Sample")
lines(inSampleLongLikelihood,col="green")
lines(inSampleShortLikelihood,col="red")
legend(x='bottomright', c("Long HMM Likelihood","Short HMM Likelihood"), fill=c("green","red"), bty='n')
dev.new()
layout(1:3)
plot(Cl(outOfSampleMktData), main="S&P 500 HMM Trend Following Out of Sample")
lines(outOfSampleLongTrendSignalForPlot,col="green",type="l")
lines(outOfSampleShortTrendSignalForPlot,col="red",type="l")
legend(x='bottomright', c("S&P 500 Closing Price","Long Signal","Short Signal"), fill=c("black","green","red"), bty='n')
#tt <- Cl(outOfSampleMktData)
#tt[,1] <- outOfSampleLongLikelihood
plot(outOfSampleLongLikelihood,main="Log Likelihood of each HMM model - Out Of Sample")
lines(outOfSampleLongLikelihood,col="green")
lines(outOfSampleShortLikelihood,col="red")
legend(x='bottomright', c("Long HMM Likelihood","Short HMM Likelihood"), fill=c("green","red"), bty='n')
#Вычисляем прибыльность для проверочной выборки
outOfSampleLongReturns <- Lag((1*(outOfSampleLongLikelihood > outOfSampleShortLikelihood)))* (outOfSampleDailyRet)
outOfSampleLongReturns[is.na(outOfSampleLongReturns)] < - 0
outOfSampleShortReturns <- Lag(-1*(1*(outOfSampleLongLikelihood < outOfSampleShortLikelihood)))* (outOfSampleDailyRet)
outOfSampleShortReturns[is.na(outOfSampleShortReturns)] <- 0
outOfSampleTotalReturns <- outOfSampleLongReturns + outOfSampleShortReturns
outOfSampleTotalReturns[is.na(outOfSampleTotalReturns)] <- 0
plot(cumsum(outOfSampleTotalReturns),main="S&P 500 HMM Trend Following Out of Sample Strategy Returns")
lines(cumsum(outOfSampleLongReturns),col="green")
lines(cumsum(outOfSampleShortReturns),col="red")
legend(x='bottomright', c("Total Returns","Long Trend Returns","Short Trend Returns"), fill=c("black","green","red"), bty='n')
print(SharpeRatio.annualized(outOfSampleTotalReturns))
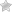


Приветствую. На часовках какие результаты ?
Еще вопрос - как перевести коэффициент правдоподобия в логарифмах в проценты ? В логарифмах не очень понятно.
Не совсем понятно, о каких процентах идет речь? Это просто значение функции максимального правдоподобия, она особой смысловой нагрузки не несет в данном случае. Если для какой-то модели она больше, чем для другой - выбирается первая, больше ничего знать тут не нужно
Коэффициент правдоподобия (лайкехуд) считает в % от оригинала, у него есть верхний предел 100%, т.е. если коэффицент 50% это значит что соответвует оригиналу на 50%. Логарифмы переводятся в%.
Автор не проводил исследования на часовых диапазонах,попробуйте проверить сами, заодно напишите результаты, получится небольшое исследование.
Почему на самом верхнем графике(назовем график N1), на аптренде идут шортовые сигналы ( с 2013 года по середину 2014 года) ?
Так определила модель на проверочной выборке. Понятно, что это может быть не совсем верно, поэтому надо эту модель усовершенствовать, либо при определении классов на обучающей выборке применять другие критерии.
Пятый, по счету график "с верху", это на аутофсемпл на реальных данных ? Правильно или ?
На реальных данных, но модель прогнали на обучающей выборке - in sample.
Обучающая выборка была сколько баров из того периода который на графике ?
Update: There was a look forward bug in the code when calculating outOfSampleLongReturns and outOfSampleShortReturns, this has been corrected and sadly reduced the sharpe ratio from 3.08 to 0.857. This is why I always publish the code to provide greater transparency than other sites
Автор статьи на английском добавил, что был баг и что прибыли нет...:-) Вопрос - эта стратегия на тех "фичах" которые перечислял автор(для "вектора состояния" может приносить прибыль или нет ? Я понял так, что на out of semple стратегия прибыль не приносит.
Автор написал, что коэффициент Шарпа понизился из-за ошибки до 0.857. Это означает что стратегия прибыльна, но прибыль несколько ниже, чем до ошибки. У меня в статье все графики и коды приведены уже с учетом исправлений.
В статье аутофсемпл убыточны. Я пока не увидел, в том числе в других публикациях, что Марковские модели работают. От вас так-же нормального ответа оне последовало - приносит ли стратегия прибыли на тестах аутофсемпл с использование тех "векторов состояний" которые использует автор.
Где вы видите, что они убыточны?
Вы хотите сказать что еквити с пятого графика это реальный аутофсемпл с "векторами автора" ?
Эквити out-of-sample показан на третьем графике сверху.
Убыточный график третий сверху, очень не интересный, зачем стратегия которая теряет деньги ? Я разбираюсь, есть ли смысл в самих Марковских моделях или нет. Код для HMM есть для C++.
Мы видимо смотрим разные графики. На третьем сверху графике черной линией показана общая прибыль стратегии. которая к концу выборки out-of-sample составила 70%.
Стратегия на аутофсемпл на аптренде , год целый , генерировала шортовые сигналы ! Это не прибыльная стратегия на аутофсемпл - график 1 и 3 это демонстрируют.
70% за 9 лет ))))) вы прикалываетесь ? )))))) Сбербанк уже больше платит.
Почему за 9 лет? Вы вообще эту статью смотрите? Там выборка с января 2010 по декабрь 2014 года. И 70 % в валюте за 5 лет - где вы такую ставку увидели в Сбербанке? Не забываете, что это демонстрационный пример , а не реально разработанная стратегия. То есть предлагается только для иллюстрации работы модели Маркова. И из него явно следует, что стратегия имеет потенциал
70% кумулятивный доход на аутофсемпл и 600% на инсемпл, 70% - похоже на статистическую ошибку.
Вы явно не понимаете разницу между обучением модели и ее тестировании на проверочной выборке
Разница между графиками 3 и 5 ощущается, стратегия выбирает 10% на аутофсемпл из возможных 600% которые есть на инсемпл.
Работа должна оплачиваться. 70% за 4 года, это не та работа которой стоит заниматься, т.к. не конкурирует с нормальными системами.
Можно немножко подумать и взять вместо минимального периода, равного 1 день, например, период , равный 1 мин.Как вы думаете, за какой срок вы получите эти 70 % в таком случае?
1. Эквити на аутофсемпл "не очень", что-бы стоило умножать на 8 и типа считать что-то на часовых графиках. 2. Эквики на инсемпл, несопоставима с аутофсемпл, и это на одном и том-же таймфрейме.
Вам не показалось перебором создавать 42 гауссиана? с точки зрения здравого смысла это мягко говоря перебор. может быть изза этого происходит переподгонка? 10 гауссианами можно все что угодно в мире описать, только будет ли от этого толк?
и еще вопрос. метод HMM с применением метода Витерби очень сильно зависит от начальных условий( состояний и их вероятностей). какие состояния задаются в данном случае как начальные?
Здравствуйте! Не могли бы Вы, пожалуйста, пояснить, как у Вас получился Log Likelihood больше нуля? Допустим, он берется со знаком минус. Тогда почему на одном графике Log Likelihood имеет разные знаки?
Под likelihood в данной работе автор имеет в виду не вероятность, которая не может превышать 1, а некоторую статистическую меру, которая у него может принимать значения и >1.
Спасибо за ответ! Я понял, что был неправ, так как считал, что функция правдоподобия всегда лежит в диапазоне от 0 до 1, что неправда. Также я заметил, что в модели присутствует BIC criterium. Как я понимаю, это байесовский критерий, который служит для сравнения моделей с разным количеством состояний. Правильно ли я понимаю, что чем BIC меньше, тем лучше модель?
Здравствуйте,
почитал статью, очень интеренсно. Я не слишком хорошо знаком именно с этим математическим аппаратом, обязатель почитаю, я хорошо в математике понимаю.
Посмотрел код и у меня возник вопрос. Правильно ли я поняла, что для обучения, например на продажу, передаются наборы из матриц переменной ширины, каждая с колонками из features, для которых сигнал равен 1. Если это так, то получается, что модель на покупку никак не учитывает данных, того факта, откуда сверху мы пришли и как пришли. Мы рассматриваем только растущий тренд от его начала и пытаемся предсказать его окончание. Странно. На мой взляд надо бы хотя бы знать некоторые цели роста, а они могут быть взяты из того падающего тренда, который был до начала роста, конец которого мы определяем. Возможно я неверно поняла код, я хорошо на C++ (типа ALGLIB), R для меня не очень знаком.
А потом при торговле мы передаем features по пять штук, и по эти пяти пытаемся что-то определить. А обучали по переменному количеству. HmmLikelihoodTestLength. Непонятно. Тогда и обучать логично по пяти. Вот это непонятно.
Все равно спасибо за статью, её перевод. Это как бы альтернатива нейронным сетям получается...
Здравствуйте! Прогнал код, параметры моделей LongModelFit и ShortModelFit почему-то не соответствуют тем, которые получились у автора. Таким образом, итоговые результаты тоже сильно отличаются.