В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый - использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
Метод первый - одна модель с несколькими состояниями.
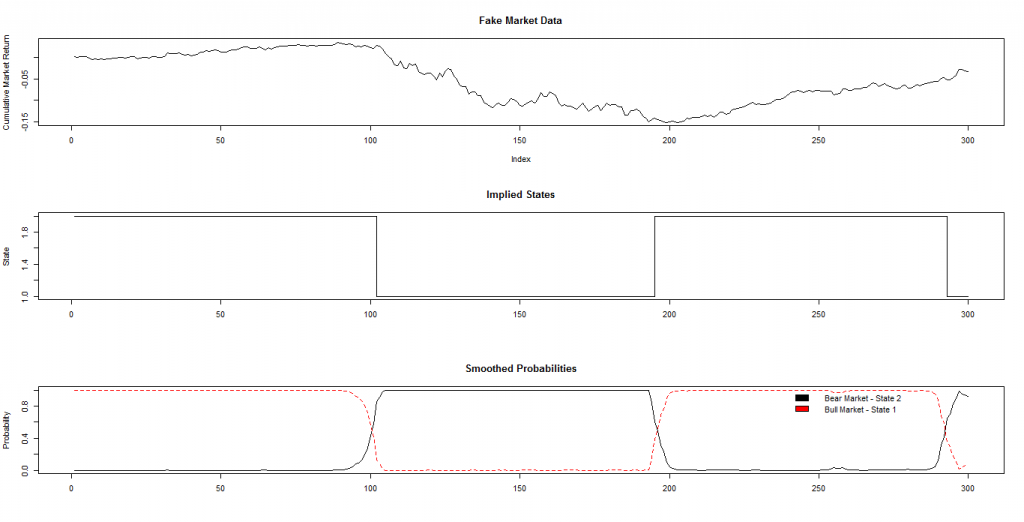
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu - медиана, sigma - среднеквадратичное отклонение. Распознавание будем производить для двух режимов - бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых - из медвежьего и 100 последних - из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
Далее показан листинг на R, в котором эти данные генерируются, а затем на них обучается модель Маркова с двумя состояниями:
###############################################################################
# Load Systematic Investor Toolbox (SIT)
# https://systematicinvestor.wordpress.com/systematic-investor-toolbox/
###############################################################################
setInternet2(TRUE)
con = gzcon(url('http://www.systematicportfolio.com/sit.gz', 'rb'))
source(con)
close(con)
#*****************************************************************
# Генерируем данные согласно описанию
#******************************************************************
bull1 = rnorm( 100, 0.10, 0.15 )
bear = rnorm( 100, -0.01, 0.20 )
bull2 = rnorm( 100, 0.10, 0.15 )
true.states = c(rep(1,100),rep(2,100),rep(1,100))
returns = c( bull1, bear, bull2 )
# Нахождение режимов
load.packages('RHmm')
y=returns
ResFit = HMMFit(y, nStates=2)
VitPath = viterbi(ResFit, y)
#Вычисляем вероятности нахождения в режимах
fb = forwardBackward(ResFit, y)
# строим график вероятностей
layout(1:2)
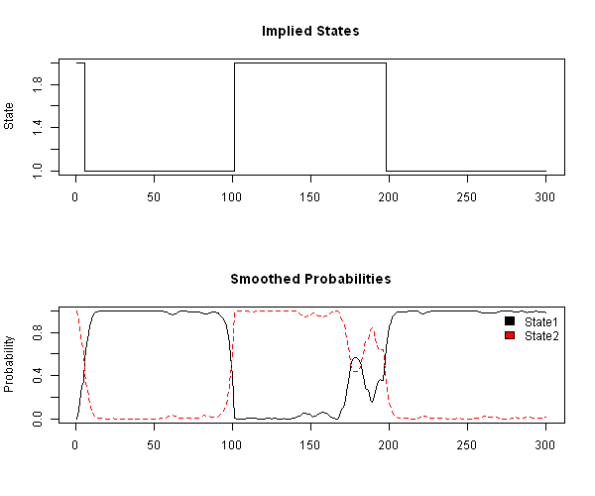
plot(VitPath$states, type='s', main='Implied States', xlab='', ylab='State')
matplot(fb$Gamma, type='l', main='Smoothed Probabilities', ylab='Probability')
legend(x='topright', c('State1','State2'), fill=1:2, bty='n')
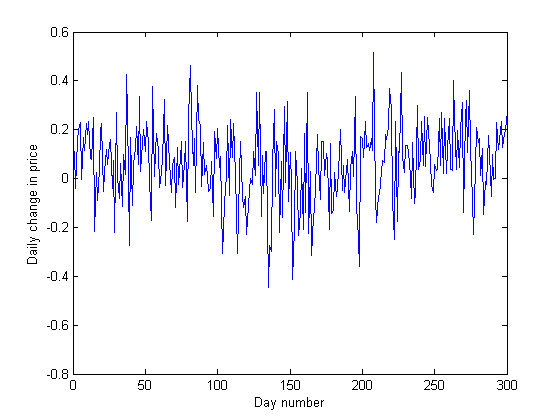
На первом графике показаны режимы, как они были заданы при генерации приращений. На втором графике - вероятности нахождения в том или ином состоянии, полученные при обучении модели Маркова при помощи выше приведенного кода.
Далее сгенерируем дополнительные данные для проверки работы модели:
#*****************************************************************
# Добавление данных для проверки работы модели
#******************************************************************
bear2 = rnorm( 100, -0.01, 0.20 )
bull3 = rnorm( 100, 0.10, 0.10 )
bear3 = rnorm( 100, -0.01, 0.25 )
y = c( bull1, bear, bull2, bear2, bull3, bear3 )
VitPath = viterbi(ResFit, y)$states
#*****************************************************************
# Строим графики
#******************************************************************
load.packages('quantmod')
data = xts(y, as.Date(1:len(y)))
layout(1:3)
plota.control$col.x.highlight = col.add.alpha(true.states+1, 150)
plota(data, type='h', plotX=F, x.highlight=T)
plota.legend('Returns + True Regimes')
plota(cumprod(1+data/100), type='l', plotX=F, x.highlight=T)
plota.legend('Equity + True Regimes')
plota.control$col.x.highlight = col.add.alpha(VitPath+1, 150)
plota(data, type='h', x.highlight=T)
plota.legend('Returns + Detected Regimes')
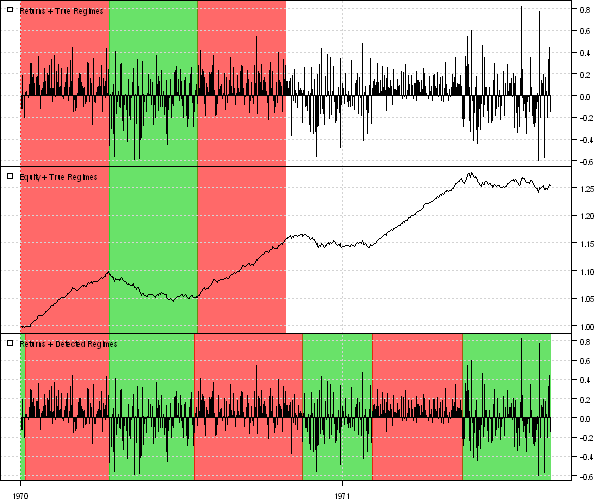 Мы использовали 300 первых наблюдений для обучения модели Маркова, 300 последующих - для проверки ее работы. На первом графике показаны сгенерированные наблюдения, цветом заданы состояния. На следующем графике - "цена" актива, где визуально можно проследить, какой тренд - бычий или медвежий - присутствует на рынке. На последнем графике цветом показано, как обученная модель определила эти режимы на проверочных данных. Как видно, модель достаточно адекватно находит состояния рынка в этом примере.
Мы использовали 300 первых наблюдений для обучения модели Маркова, 300 последующих - для проверки ее работы. На первом графике показаны сгенерированные наблюдения, цветом заданы состояния. На следующем графике - "цена" актива, где визуально можно проследить, какой тренд - бычий или медвежий - присутствует на рынке. На последнем графике цветом показано, как обученная модель определила эти режимы на проверочных данных. Как видно, модель достаточно адекватно находит состояния рынка в этом примере.
Метод два - несколько моделей Маркова, одна для каждого режима.
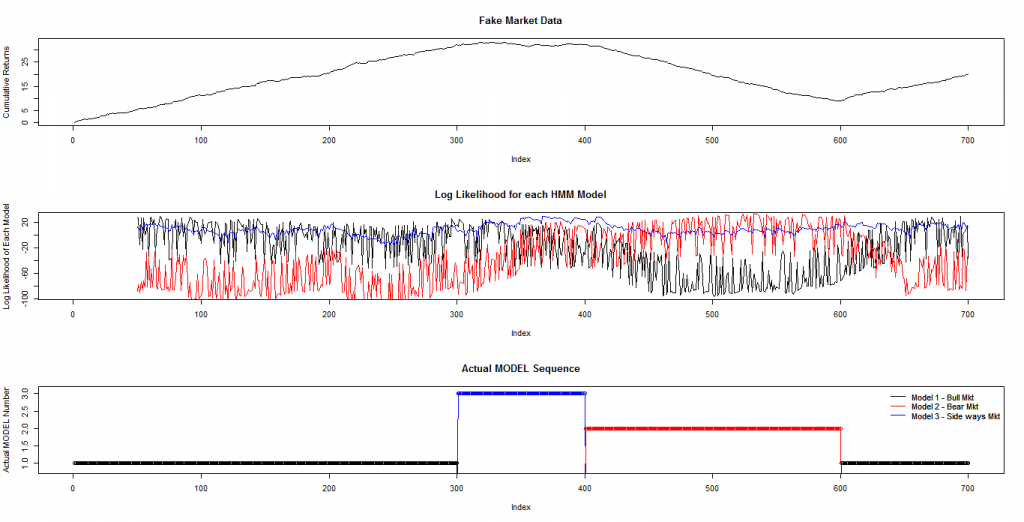
В данном случае симулируем три режима рынка - бычий, медвежий и боковик. Будем обучать три модели Маркова с двумя состояниями для каждого режима: НММ1 - для бычьего рынка, НММ2 - для медвежьего рынка, НММ3 - для боковика. Скользящее окно из 50 значений приращений ( 50 дней) пропущено через них и получен логарифм вероятности соответствия данных модели и исходных данных:
На первом графике показаны кумулятивные приращения - "цена" актива. На втором - вычисленные логарифмы вероятностей для каждой из 3 моделей. На последнем - исходные режимы рынка. Как видно из этих графиков, достаточно четко модель различает бычий и медвежий режимы, но для бокового состояния рынка разница не столь очевидна, модель Маркова для боковика показывает стабильно высокую вероятность во всех режимах.
Ниже приведен листинг для второго метода:
library('RHmm') #Load HMM package
library('zoo')
#HMM модель 1 ( высокая волатильность и низкая волатильность для бычьего тренда)
model1ReturnsFunc < - function(isHighVol){
return(rnorm( 100, 0.1,if(isHighVol){0.15}else{0.02}))
}
bullLowVol = model1ReturnsFunc(F)
bullHighVol = model1ReturnsFunc(T)
model1TrainingReturns = c(bullLowVol, bullHighVol)
Model1Fit = HMMFit(model1TrainingReturns, nStates=2) #Fit a HMM with 2 states to the data
#HMM модель 2 (высокая и низкая волатильность для медвежьего тренда)
model2ReturnsFunc <- function(isHighVol){
return(rnorm( 100, -0.1,if(isHighVol){0.15}else{0.02}))
}
bearLowVol = model2ReturnsFunc(F)
bearHighVol = model2ReturnsFunc(T)
model2TrainingReturns = c(bearLowVol, bearHighVol)
Model2Fit = HMMFit(model2TrainingReturns, nStates=2) #Fit a HMM with 2 states to the data
#HMM модель 3 (боковик)
model3ReturnsFunc <- function(isHighVol){
return(rnorm( 100, 0.0,if(isHighVol){0.16}else{0.08}))
}
sidewaysLowVol = model3ReturnsFunc(F)
sidewaysHighVol = model3ReturnsFunc(T)
model3TrainingReturns = c(sidewaysLowVol, sidewaysHighVol)
Model3Fit = HMMFit(model3TrainingReturns, nStates=2) #Fit a HMM with 2 states to the data
generateDataFunc <- function(modelSequence,highVolSequence){
results <- c()
if(length(modelSequence) != length(highVolSequence)){ print("Model Sequence and Vol Sequence must be the same length"); return(NULL)}
for(i in 1:length(modelSequence)){
if(modelSequence[i] == 1){
results <- c(results,model1ReturnsFunc(highVolSequence[i]))
}
if(modelSequence[i] == 2){
results <- c(results,model2ReturnsFunc(highVolSequence[i]))
}
if(modelSequence[i] == 3){
results <- c(results,model3ReturnsFunc(highVolSequence[i]))
}
}
return(results)
}
#создаем выборку out-of-sample
actualModelSequence <- c(1,1,1,3,2,2,1)
actualVolRegime <- c(T,T,T,T,T,T,T)
outOfSampleData <- generateDataFunc(actualModelSequence,actualVolRegime)
#берем 50 дней данных и вычисляем скользящий логарифм вероятности для каждой модели
model1Likelihood <- rollapply(outOfSampleData,50,align="right",na.pad=T,function(x) {forwardBackward(Model1Fit,x)$LLH})
model2Likelihood <- rollapply(outOfSampleData,50,align="right",na.pad=T,function(x) {forwardBackward(Model2Fit,x)$LLH})
model3Likelihood <- rollapply(outOfSampleData,50,align="right",na.pad=T,function(x) {forwardBackward(Model3Fit,x)$LLH})
layout(1:3)
plot(cumsum(outOfSampleData),main="Fake Market Data",ylab="Cumulative Returns",type="l")
plot(model1Likelihood,type="l",ylab="Log Likelihood of Each Model",main="Log Likelihood for each HMM Model")
lines(model2Likelihood,type="l",col="red")
lines(model3Likelihood,type="l",col="blue")
plot(rep((actualModelSequence==3)*3,each=100),col="blue",type="o",ylim=c(0.8,3.1),ylab="Actual MODEL Number",main="Actual MODEL Sequence")
lines(rep((actualModelSequence==2)*2,each=100),col="red",type="o")
lines(rep((actualModelSequence==1)*1,each=100),col="black",type="o")
legend(x='topright', c('Model 1 - Bull Mkt','Model 2 - Bear Mkt','Model 3 - Side ways Mkt'), col=c("black","red","blue"), bty='n',lty=c(1,1,1))
В следующей статье цикла будем обучать модель и оценивать ее применяемость на данных реального рынка.
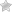


На реальных данных работает ?
Конечно, в следующей части это будет продемонстрировано.
Обучение идет на выборке, а на аутофсемпл торговля ? Не ли подгонки ? На каком периоде производится обучение состояний ?
Да, сначала обучение ( 300 значений в первом методе), затем проверка out of sample (тоже 300 приращений). Понятие подгонки существует для случаев, когда используется какая-то эмпирическая зависимость, никак не подтвержденная теоретически. Для математических моделей имеет смысл говорить только о робастности - насколько модель отражает реальные события, поэтому - подгонки нет.
Да, интересно будет прогнать код и посмотреть результат. Кстати, автор блога как следует из комментариев, нашел ошибку в коде, которая неправомерно улучшала результаты тестирования. Разницу можно наблюдать , если сравнить графики oos в нормальном размере и увеличенном, к сожалению, после корректировки кода все стало заметно хуже
Я опубликую результаты автора уже с учетом исправлений
Добрый день!
Допустим, я натреировал модель на каком-то тестовом периоде. Как мне в режиме реального времени определять, в каком состоянии (1 или 2) я нахожусь?
Я использую пакет MS_Regress для matlab отсюда: http://blogs.mathworks.com/pick/2011/02/25/markov-regime-switching-models-in-matlab/
И не совсем понимаю, что мне делать после того, как я натренировал модель.
Буду признателен если разъясните!
Ну если у вас есть обученная модель, то подавайте на ее вход входные данные, как вы делали при обучении, и на выходе должны получить, к какому режиму относится состояние рынка. Я не знаю, как работает в Матлабе модель, но у меня классификатор HMM сразу выдает номер режима или класса.