В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность данных полученных моделью по всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность данных полученных моделью по одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности 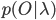 . Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
. Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
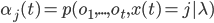
Это выражение вычисляется рекурсивно через форвардную переменную в момент времени t-1 , находясь в состоянии k, и затем вычисляется состояние j в момент времени t:
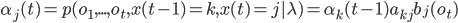
где 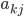 - вероятность перехода из состояния k в состояние j, и
- вероятность перехода из состояния k в состояние j, и 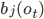 - вероятность генерации вектора параметров
- вероятность генерации вектора параметров 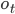 из состояния t.
из состояния t.
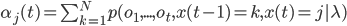
1. Инициализация алгоритма.
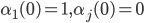 для
для 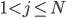 и
и 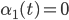 для
для 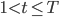
2. Рекурсия.
Для 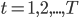
.........для 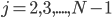
................![\alpha_j(t)=b_j(o_t)[\sum_{k=1}^{N-1}\alpha_k(t-1)a_{kj}]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_fcde78eb7cb346b51c97f7adc995f777.gif)
3. Решение.
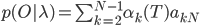
Алгоритм Витерби.
Форвардный алгоритм находит 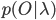 суммированием по всем возможным последовательностям состояний, но иногда предпочтительней аппроксимировать
суммированием по всем возможным последовательностям состояний, но иногда предпочтительней аппроксимировать 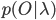 вероятностью
вероятностью 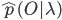 которая вычисляется для одной, наиболее вероятной последовательности. Для этого применяется алгоритм Витерби:
которая вычисляется для одной, наиболее вероятной последовательности. Для этого применяется алгоритм Витерби:
![\hat{p}(O|\lambda)=\max_X[p(O,X|\lambda)]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_41298816bc046701376316b54ef1b7db.gif) , где X - наиболее вероятная последовательность состояний.
, где X - наиболее вероятная последовательность состояний.
Вероятность лучшего пути длиной t по модели Маркова, заканчивающегося состоянием j определяется как:
![\phi_j(t)=\max_{X^{t-1}}[p(o_1,...,o_t, x(t)=j|\lambda)]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_f6d70a1071c6522f47acf595c63797bd.gif) , где
, где 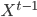 - лучший путь/последовательность состояний.
- лучший путь/последовательность состояний.
Форвардная переменная 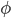 также может быть вычислена рекурсивно:
также может быть вычислена рекурсивно:
![\phi_j(t)=\max_i[\phi_i(t-1)a_{ij}b_j(o_t)]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_f71d1e6f28d6f6cb689e0d53514a192a.gif)
1. Инициализация алгоритма.
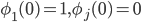 для
для 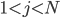 и
и 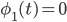 для
для 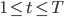
2. Рекурсия.
Для 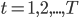
...........для 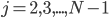
.....................![\phi_j(t)=\max_{1\leq k<N}[\phi_k(t-1)a_{kj}]b_j(o_t)](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_5d142f1a27c8d6172ef4d5e6ff09f99d.gif)
...................................сохранить предыдущее значение 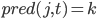
3. Решение.
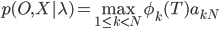
сохранить предыдущее значение 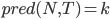 .
.
Наилучший путь находится путем следования по сохранненым значениям в обратном порядке по 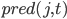 .
.
Ошибки малой разрядности
Прямое вычисление 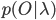 может привести к ошибкам малой разрядности. Значение вероятности может быть таким маленьким, что компьютер не сможет рассчитать его верно. Вместо этого необходимо использовать вычисление натурального логарифма
может привести к ошибкам малой разрядности. Значение вероятности может быть таким маленьким, что компьютер не сможет рассчитать его верно. Вместо этого необходимо использовать вычисление натурального логарифма 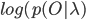 .
.
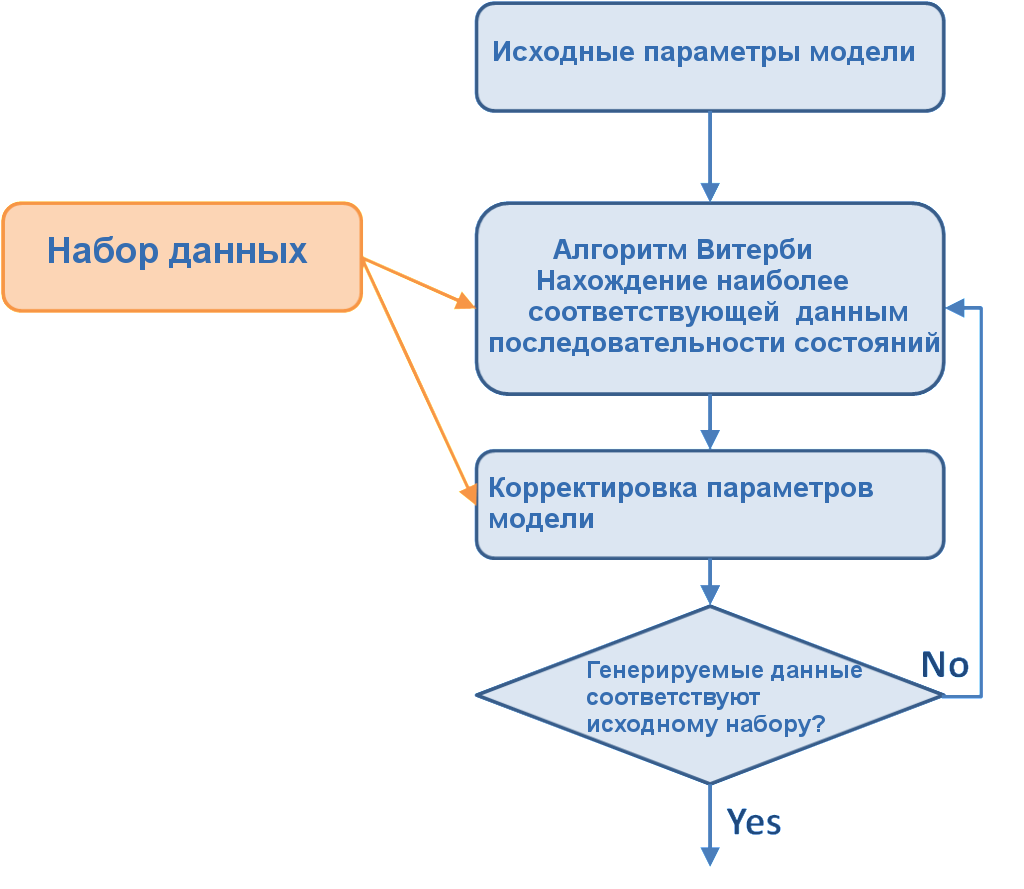
В следующей части цикла рассмотрим тренировку модели Маркова на сгенерированных входных данных с помощью реализации разобранных выше алгоритмов на языке R.


Спасибо за интересные переводы и исследования. А можно вас попросить еще и на сайт www.long-short.ru кросспосты делать?
Можно, в том случае, если в тексте статьи можно оставлять ссылки на мой сайт.
Разумеется можно.
Конечно, в следующей части это будет показано