QuantAlgos

Трейдеры, которые приобрели мою программу robot_uralpro, спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея "одноногого" статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется "lead-lag relationship" -опережение-отставание между разными активами.

Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.

Могу сразу отметить, что на современной бирже в большинстве случаев изменение цены фьючерса в направлении последующего движения рынка происходит раньше, чем изменение значения синтетического индекса. Объясняется это тем, что фьючерс торгуется активнее, его волатильность больше, порог входа  меньше. Однако это знание ничего не дает в плане построения алгоритма, потому что нам надо точно определить, когда эти случаи происходят, сколько времени длятся, и когда все-таки индекс начинает идти вперед. Обычно для этого предлагается использовать кросс-ковариацию приращений цен активов, получаемую путем расчета ковариации, когда выборка приращений цен одного из активов сдвинута во времени на некоторую величину , называемую лагом:

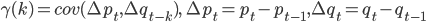$\gamma(k)=cov(\Delta p_t,\Delta q_{t-k}), \;\Delta p_t=p_t-p_{t-1}, \Delta q_t=q_t-q_{t-1}$, где

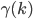$\gamma(k)$ - кросс-ковариация для лага k;

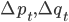$\Delta p_t,\Delta q_t$ - текущие приращения цен первого и второго активов.

Если кросс-ковариация положительна при положительном k, то делается вывод, что актив q опережает актив p, если кросс-ковариация положительна при отрицательном k, то актив p опережает актив q.

Однако правильное вычисление кросс-ковариации возможно, если данные о приращении цены поступают через равные интервалы времени t и не содержат пропусков . Ни то, ни другое условие не выполняется для высокочастотных данных, которые требуются для HFT и просто intraday алгоритмов. Обычно эту проблему решают так - разбивают выборку на равные интервалы и если между ними не происходило изменение цены, то полагают приращение цены равным 0. Это приводит к сильной зависимости ковариации от частоты разбиения и в общем к неправильному ее вычислению в динамическом режиме. Кроме того, ковариация зависит и от величины приращения цен, что в случае большой разницы между ценами активов, также приводит к неверным результатам.

Более точный подход к определению lead-lag relationship предлагают авторы работы "Intraday Lead-Lag Relationships between the Futures-, Options and Stock Market". Для получения правильного значения кросс-ковариации берутся приращения цен, взятые между двумя наблюдениями , между которыми может быть более одного изменения цены. Рассмотрим всю процедуру вычисления более подробно.

Обозначим наблюдения цены 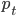$p_t$ индексом i, цены 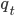$q_t$ индексом j, и общее число наблюдений N и M соответственно. Разница между двумя разными уровнями цены может быть записана как сумма приращений ненаблюдаемого процесса изменения цены в интервале между наблюдениями:

$p_{t_{i+1}}-p_{t_i}=\sum_{t=t_i+1}^{t_{i+1}}\Delta p_t$

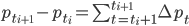
где 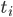$t_i$ означает временную метку i-го наблюдения. Кросс-произведение приращения цен между двумя активами запишем как:

$y_{ij}=(p_{t_{i+1}}-p_{t_i})(q_{t_{j+1}}-q_{t_j})=\sum_{t=t_i+1}^{t_{i+1}}\Delta p_t\sum_{t=t_j+1}^{t_{j+1}}\Delta q_s$

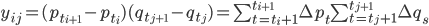
Математическое ожидание этого кросс-произведения есть линейная комбинация кросс-ковариаций:

$E(y_{ij}|t_i,t_j,t_{i+1},t_{j+1})=E(\sum_{t=t_i+1}^{t_{i+1}}\Delta p_t\sum_{t=t_j+1}^{t_{j+1}}\Delta q_s)=\sum_{t=t_i+1}^{t_{i+1}}\sum_{t=t_j+1}^{t_{j+1}}\gamma(t-s)$

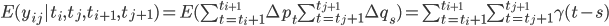
и это выражение зависит от наблюдаемых моментов времени 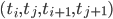$(t_i,t_j,t_{i+1},t_{j+1})$. Далее обозначим 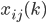$x_{ij}(k)$ число раз, когда 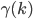$\gamma(k)$ появляется в выше приведенном выражении:

$x_{ij}(k)=\max(0,\min(t_{i+1},t_{j+1}+k)-\max(t_i,t_j+k))$.

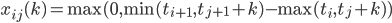Важной особенностью 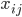$x_{ij}$ является то, что эти значения зависят только от моментов времени наблюдаемых изменений цены 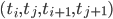$(t_i,t_j,t_{i+1},t_{j+1})$ и не зависят от цены активов. Таким образом,мы можем записать 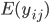$E(y_{ij})$ как линейную комбинацию ковариаций $\gamma(k),\;k=-K...K$:

$E(y_{ij}|x_{ij})=\sum_{k=-K}^K x_{ij}(k)\gamma(k)$

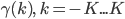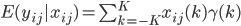
Вышеприведенное выражение может рассматриваться как выражение регрессии с неизвестными кросс-ковариациями 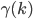$\gamma(k)$ в виде параметров и коэффициентами 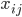$x_{ij}$ в виде объясняющих переменных. В векторной записи:

$y_{ij}=x_{ij}^{`}\gamma+e_{ij}$.

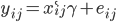Таким образом, кросс-ковариации могут быть вычислены методом наименьших квадратов по наблюдениям 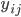$y_{ij}$ и рассчитанным значениям $x_{ij}$.

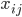В рассмотренном методе могут быть использованы любые интервалы между наблюдаемыми ценами, в зависимости от требуемой вами частоты сделок. Также достаточно ограничиться интервалами, где 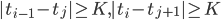$|t_{i-1}-t_j|\geq K,|t_i-t_{j+1}|\geq K$, где К - максимальный требуемый лаг.

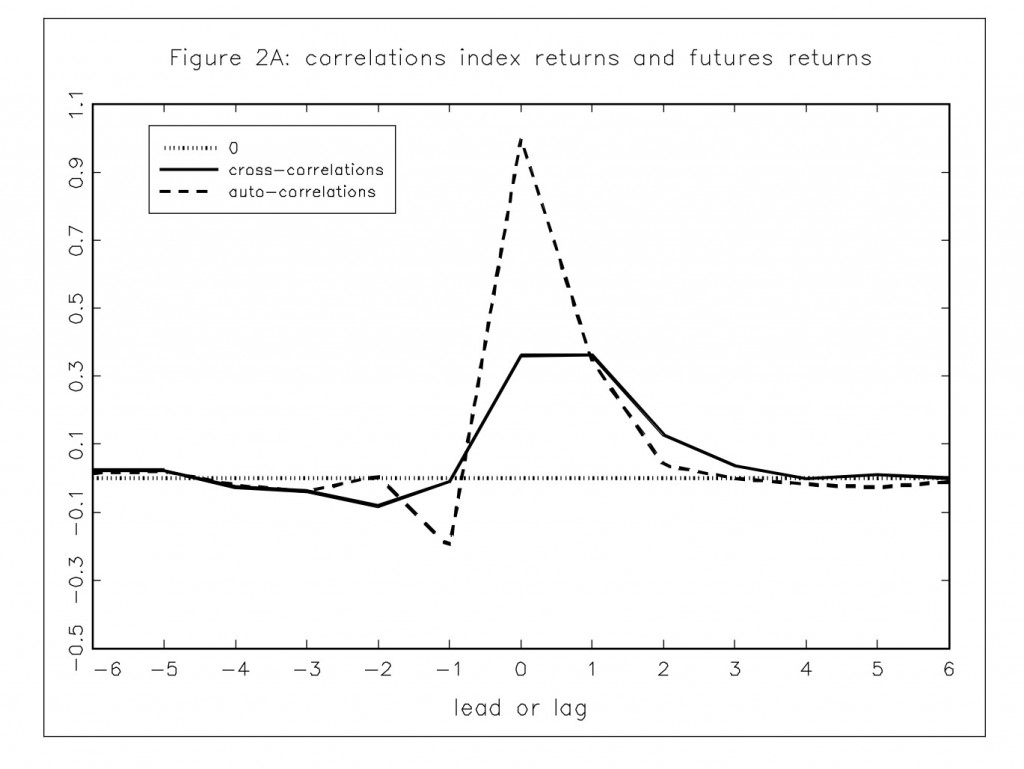
В заглавии поста приведен график кросс корелляции между приращениями цены индекса AEX амстердамской биржи и фьючерса на этот индекс. Минимальный шаг лага k взят равным пяти минутам. Максимальное значение K=6, то есть приращения цен измеряются внутри пересекающегося интервала длительностью 30 мин. Из этого графика видно, что на интервалах от 0 до 15 минут фьючерс опережает индекс с максимальным значением корреляции в районе 5 мин.

Кстати, очень перспективно выявления lead-lag relationship между фьючерсом и его опционами. Кто сможет правильно произвести все вычисления, получит очень интересный алгоритм статистического арбитража.

Также дам рекомендацию тем, кто улучшает алгоритм robot_uralpro. Не стремитесь к очень высокой частоте сделок, увеличьте немного интервалы расчетов, там уйдут многие микроструктурные особенности, которые и не учитывались в 2010 году этой стратегией, но имеют сильное влияние сейчас. Это значительно облегчит вашу работу. Но помните, что слишком большой интервал между сделками тоже приведет к уменьшению статистической достоверности. По моим испытаниям этого алгоритма в тестировании на современных данных выходило около 500 сделок в день при объеме 5 контрактов RI, ориентируйтесь на это значение.