QuantAlgos

В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R.

Рабочая среда распознавания основных паттернов.

Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:

$\hat{w}=\arg\max_w P(w|O)$

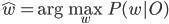
Так как 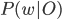$P(w|O)$ неизвестен, применяем правило Байеса:

$\hat{w}=\arg\max_w\frac{P(O|w)P(w)}{P(O)}=\arg\max_w P(O|w)P(w)$

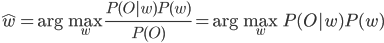
Максимизация не зависит от 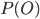$P(O)$, поэтому мы можем игнорировать эту вероятность. 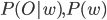$P(O|w), P(w)$ означают вероятность того, что данные O принадлежат классу w и вероятность существования класса w соответственно. 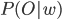$P(O|w)$ определяется моделью скрытых состояний Маркова.

Формулировка задачи.

Сначала нам нужно сгенерировать набор признаков О из рыночных данных d. Пока пропустим этот шаг, потому что он будет различаться для разных применений модели Маркова, например для финансов d может быть представлен ценами разных активов и О можно обозначить набор технических индикаторов, применяемых к d. Модель Маркова также популярна в задачах распознавания речи, где О обычно является вектором, описывающим характеристики частотного спектра речи.

Затем необходимо вектор О ассоциировать с классом модели Маркова. Это можно сделать путем применения метода максимального правдоподобия, где модель Маркова определяет класс, который с наибольшей вероятностью генерирует набор параметров, соответствующий набору параметров О.

Спецификация модели Маркова.

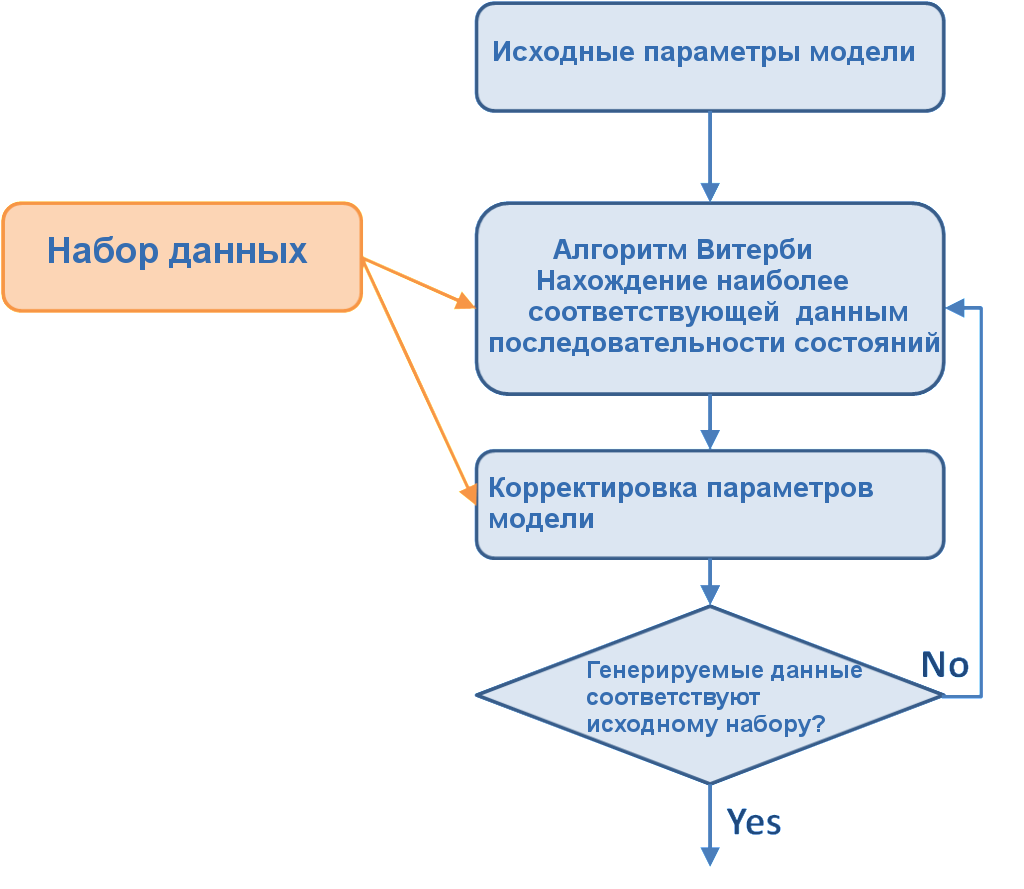
Рассмотрим рисунок в заглавии поста. На нем приведены следующие обозначения:

N - число состояний модели (на рисунке равно 5),

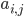$a_{i,j}$ - вероятности перехода из состояния i в состояние j,

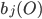$b_j(O)$ - вероятность получения вектора параметров О при состоянии j ( j не является входным и выходным состоянием),

вектор параметров модели Маркова 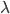$\lambda$ определим как $\lambda=[N,a_{i,j},b_j]$,

$O=[o_1,o_2,...,o_T]$ - вектор параметров наблюдений,

$X=[x_1,x_2,..,x_T]$ - найденный вектор последовательности состояний.

Совместная вероятность соответствия вектора О последовательности состояний X при параметрах модели 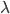$\lambda$ равна вероятности перехода  из текущего состояния в следующее , умноженное на вектор параметров, сгенерированный в этом состоянии:

$p(O,X|\lambda)=a_{x_0,x_1}\prod_{t=1}^T b_{x_t}(o_t)a_{x_t,x_{t+1}}$

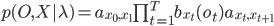
где 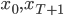$x_0,x_{T+1}$ - входное состояние 1 и выходное сотояние N соответственно.

Вычисление вероятности.

В рассмотренной выше совместной вероятности мы определили последовательность состояний X. Так как эта последовательность является скрытой переменной ( вот почему модель Маркова называется моделью скрытых состояний), мы ее не знаем. Однако, если мы суммируем вероятности по всем возможным состояниям, то получим:

$p(O|\lambda)=\sum_X p(O,X|\lambda)$

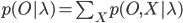
Это может быть проблематичным из-за большого числа состояний модели (особенно в приложениях реального времени), но существуют эффективные алгоритмы для такого вычисления, без нахождения каждого отдельного состояния. Подобным алгоритмом является форвардный алгоритм.

Что представляет из себя 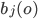$b_j(o)$?

Это полученное распределение вероятностей при состоянии j модели. Это распределение может быть любым, но оно должно соответствовать распределению данных при состоянии j, и должно быть математически определяемым. Обычным выбором на этой стадии является предположение, что вектор O может описываться набором гауссовских распределений - мультивариантным нормальным распределением. В качестве предупреждения отметим, что если составляющие вектора параметров сильно коррелированы между собой, тогда 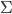$\Sigma$ - ковариационная матрица - будет иметь много вычисляемых значений. В этом случае нужно подбирать вектор парметров так, чтобы 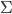$\Sigma$ представляла собой диагональную матрицу, другими словами, параметры не должны быть кореллированы между собой:

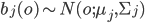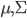$b_j(o)\sim N(o;\mu_j,\Sigma_j)$, где $\mu,\Sigma$ - параметры мультивариантного гауссовского распределения.

Как получить 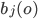$b_j(o)$? Определение параметров методом Витерби.

Мы знаем, что для описания нормального распределения достаточно методом максимального правдоподобия вычислить среднее распределения 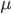$\mu$ и ковариацию 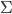$\Sigma$ вектора параметров. Значит мы должны получить только среднее и ковариацию вектора параметров для состояния j нашей модели, используя так называемую сегментацию Витерби. Она подразумевает нахождения жесткого соответствия между ветором параметров и последовательностью состояний, которое его генерировало. Существует также и альтернативный метод Баума-Вельша, который ассоциирует вектор параметров с несколькими последовательностями состояний с определенной вероятностью.

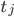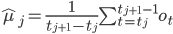
Состояние j генерирует наблюдения, начиная с $t_j$:

$\hat{\mu}_j=\frac{1}{t_{j+1}-t_j}\sum_{t=t_j}^{t_{j+1}-1}o_t$

$\hat{\Sigma}_j=\frac{1}{t_{j+1}-t_j}\sum_{t=t_j}^{t_{j+1}-1}[(o_t-\hat{\mu}_j)(o_t-\hat{\mu}_j)^{`}]$

Наперед неизвестно, какая последовательность какой вектор наблюдений генерирует, но существует алгоритм Витерби, позволяющий решить эту проблему с некоторым приближением:

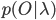Подробно алгоритм Витерби, а также форвардный алгоритм для эффективного вычисления $p(O|\lambda)$ рассмотрим в следующей части.