Продолжаем рассматривать алгоритмы построения улыбки волатильности. В этой статье будем находить "справедливые" цены опционов при помощи модели Хестона, которая относится к так называемым моделям стохастической волатильности. Хестон предложил использовать в качестве модели базового актива систему следующих уравнений:
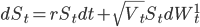
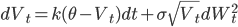
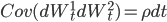 ,
,
где 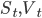 - цена и волатильность базового актива соответственно,
- цена и волатильность базового актива соответственно, 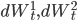 - случайные броуновские процессы с корреляцией
- случайные броуновские процессы с корреляцией 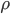 .
. 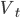 - это квадратичный процесс с возвратом к среднему (mean reverting) со средним значением
- это квадратичный процесс с возвратом к среднему (mean reverting) со средним значением 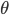 и интенсивностью k.
и интенсивностью k. 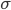 - среднеквадратичное отклонение волатильности, r - безрисковая ставка (для маржируемых равна 0, поэтому исключим сразу этот параметр для российского рынка).
- среднеквадратичное отклонение волатильности, r - безрисковая ставка (для маржируемых равна 0, поэтому исключим сразу этот параметр для российского рынка).
Реальное статистическое распределение приращений цен базового актива плохо соответствует Гауссовскому распределению, на основе которого была получена формула Блэка-Шоулза. Модель Хестона может описывать разные стат. распределения , например, коэффициент 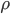 может быть интерпретирован как корелляция между логарифмом приращения цены и волатильностью актива, что позволяет учитывать эффект "толстых хвостов" распределения. График плотности распределения приращения цены с разными значениями
может быть интерпретирован как корелляция между логарифмом приращения цены и волатильностью актива, что позволяет учитывать эффект "толстых хвостов" распределения. График плотности распределения приращения цены с разными значениями 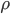 приведен в заглавии поста.
приведен в заглавии поста.
Цена европейского колл опциона для модели Хестона вычисляется по формуле:
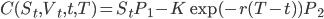 , где
, где
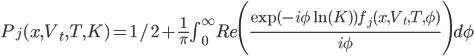
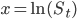
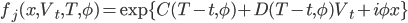
![C(T-t,\phi)=r\phi i r+\frac{a}{\sigma^2}[(b_j-\phi\sigma\phi i+d)\tau-2\ln(\frac{1-g\exp(dr)}{1-g})]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_fdf45fe79834e29def272ddb85efaac0.gif)
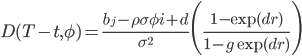
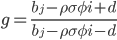
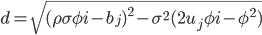
для j=1,2, где
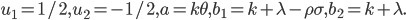
Этот набор формул кажется сложным, однако решить их достаточно просто с помощью программы на C#, которая будет приведена ниже. Сложность составляет только вычисление интеграла с верхним бесконечным пределом в формуле для 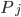 , который находится с помощью числового метода Гаусса-Лагендре в той же программе. Также, для упрощения, можно сократить число параметров, убрав из них меру риска
, который находится с помощью числового метода Гаусса-Лагендре в той же программе. Также, для упрощения, можно сократить число параметров, убрав из них меру риска 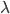 , применив риск-нейтральный подход. В этом случае:
, применив риск-нейтральный подход. В этом случае:
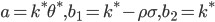
Функция расчета формулы Хестона на языке C#:
//a-нижний предел интеграла (равен 0)
//b - верхний предел интеграла. Выбирается значение от 100 до 200, в зависимости от нужной точности
//delta - вычисляется грек дельта, который равен значению Р1 в формуле Хестона
double HestonCallGaussLegendre(double S,double K,double T,double r,double kappa,double theta,
double sigma,double lambda,double v0,double rho,int trap,
double a, double b,ref double delta)
{
// Числовое интегрирование
double[] int1=new double[32];
double[] int2 = new double[32];
double y;
for (int k=0; k< =31; k++) {
y = (a + b) / 2.0 + (b - a) / 2.0 * X[k];
int1[k] = W[k]*HestonCF(y,S,K,r,T,rho,kappa,theta,lambda,sigma,v0,1,trap);
int2[k] = W[k]*HestonCF(y,S,K,r,T,rho,kappa,theta,lambda,sigma,v0,2,trap);
}
// Векторы для интегральной суммы
double I1 = VectorSum(int1);
double I2 = VectorSum(int2);
// Определение Р1 и Р2
double P1 = 0.5 + 1.0/Math.PI*I1*(b-a)/2;
double P2 = 0.5 + 1.0/Math.PI*I2*(b-a)/2;
delta = P1;
// Цена колл опциона
return S*P1 - K*P2;
}
// Функция суммирования элементов вектора
double VectorSum(double[] A)
{
double sum = 0;
double n = A.Length;
for (int i = 0; i <= n - 1; i++)
sum += A[i];
return sum;
}
private double HestonCF(Complex phi, double Spot, double Strike,
double Rate, double T, double Rho, double Kappa,
double Theta, double Lambda, double Sigma, double V,
int Pnum, int trap)
{
Complex S=new Complex(Spot , 0.0); // Цена базового актива
Complex K=new Complex(Strike, 0.0); // Страйк
Complex r=new Complex(Rate , 0.0); // Безрисковая ставка (для марж. опционов =0)
Complex tau=new Complex(T , 0.0); // Период до экспирации в долях года
Complex i=new Complex(0.0 , 1.0); // Мнимая переменная
Complex rho=new Complex(Rho , 0.0); // Параметр Хестона: Корреляция
Complex kappa = new Complex(Kappa, 0.0); // Параметр Хестона: Скорость возврата
Complex theta = new Complex(Theta, 0.0); // Параметр Хестона: уровень возвратности
Complex lambda = new Complex(Lambda, 0.0); // Параметр Хестона: мера риска (равна 0 для риск-нейтрального подхода)
Complex sigma = new Complex(Sigma, 0.0); // Параметр Хестона: Среднеквадратичное волатильности
Complex v0 = new Complex(V, 0.0); // Параметр Хестона: Текущая волатильность
Complex two=new Complex(2.0 , 0.0); // число 2 в комплексной форме
Complex one = new Complex(1.0, 0.0); // число 1 в комплексной форме
Complex y, a, u, b, sigma2, d, g, G, C, D, c, f;
y = rho*sigma*phi*i;
a = kappa*theta;
if (Pnum==1)
{
// Первая характеристическая функция
u = 0.5;
b = kappa + lambda - rho*sigma;
}
else
{
// Вторая характеристическая функция
u = -0.5;
b = kappa + lambda;
}
sigma2 = Complex.Pow(sigma,2);
d = Complex.Sqrt((y-b)*(y-b) - sigma2*(two*u*phi*i - phi*phi));
g = (b - y + d)/(b - y - d);
if (trap==1)
{
// Версия модели "Little Heston Trap"
c = one/g;
G = (one - c*Complex.Exp(-d*tau))/(one - c);
C = r*i*phi*tau + a/sigma2*((b - rho*sigma*i*phi - d)*tau - two*Complex.Log(G));
D = (b - rho * sigma * i * phi - d) / sigma2 * ((one - Complex.Exp(-d * tau)) / (one - c * Complex.Exp(-d * tau)));
}
else
{
// Оригинальный вариант Хестона
G = (one - g * Complex.Exp(d * tau)) / (one - g);
C = r*i*phi*tau + a/sigma2*((b - rho*sigma*i*phi + d)*tau - two*Complex.Log(G));
D = (b - rho * sigma * i * phi + d) / sigma2 * ((one - Complex.Exp(d * tau)) / (one - g * Complex.Exp(d * tau)));
}
f = Complex.Exp(C + D*v0 + i*phi*Complex.Log(S));
// Вычисление реальной части подинтегрального выражения
return (Complex.Exp(-i*phi*Complex.Log(K))*f/i/phi).Real;
}
Следующий шаг - определение пяти параметров 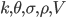 (V - текущая волатильность). Для этого нужно откалибровать модель по наблюдаемым рыночным ценам опционов. Применяем стандартный метод - берем выборку цен для опционов разных страйков за определенный период времени (вместе со сроками до экспирации), при этом рыночной ценой опциона считаем среднюю цену между бидом и аском (
(V - текущая волатильность). Для этого нужно откалибровать модель по наблюдаемым рыночным ценам опционов. Применяем стандартный метод - берем выборку цен для опционов разных страйков за определенный период времени (вместе со сроками до экспирации), при этом рыночной ценой опциона считаем среднюю цену между бидом и аском (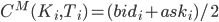 , и минимизируем следующее выражение, применяя нелинейный метод наименьших квадратов (МНК):
, и минимизируем следующее выражение, применяя нелинейный метод наименьших квадратов (МНК):
![\min S(\Omega)=\min_{\Omega}\sum_{i=1}^{N}w_i[C_i^{\Omega}(K_i,T_i)-C_i^M(K_i,T_i)]^2\leq\sum_{i=0}^Nw_i[bid_i-ask_i]^2](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_38af1f2d98dc56723252fdfedf06a7b1.gif)
где 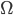 - вектор параметров,
- вектор параметров, 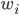 - задаваемые веса (их выбор обсудим позже), N - размер выборки. Выражение в правой части означает,что полученные значения должны попадать в промежуток между бидом и аском наблюдаемых рыночных цен. Это ограничение, равно как и условие
- задаваемые веса (их выбор обсудим позже), N - размер выборки. Выражение в правой части означает,что полученные значения должны попадать в промежуток между бидом и аском наблюдаемых рыночных цен. Это ограничение, равно как и условие 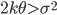 (волатильность не может падать до 0) позволяет сузить диапазон решений, полученных с помощью МНК. Таких решений может быть несколько из-за того, что МНК, попадая в локальный минимум выражения
(волатильность не может падать до 0) позволяет сузить диапазон решений, полученных с помощью МНК. Таких решений может быть несколько из-за того, что МНК, попадая в локальный минимум выражения 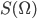 , останавливается и выдает не оптимальные значения. Таким образом, нахождение оптимальных параметров модели Хестона является нетривиальной задачей, и применяются следующие способы ее решения:
, останавливается и выдает не оптимальные значения. Таким образом, нахождение оптимальных параметров модели Хестона является нетривиальной задачей, и применяются следующие способы ее решения:
-
сделать множество вычислений с помощью МНК, задавая различные значения начальных параметров, а затем выбрать минимальное из всех полученых
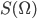 , получив таким образом соответствующие ему параметры модели;
, получив таким образом соответствующие ему параметры модели;
- применить алгоритмы поиска глобального минимума, такие, как Differential Evolution, ASA и т.п. Недостаток таких алгоритмов в значительном времени, требуемом для нахождения параметров.
Веса можно задать в соответствии с формулой : 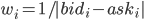 . Это интуитивный выбор, основанный на том, что, чем шире спред, тем больше свобода выбора в значении цены опциона. Для российского рынка лучшая аппроксимация получалась у меня при выборе одинакового значения весов, равного 1, но я не брал в рассмотрение слишком дальние страйки.
. Это интуитивный выбор, основанный на том, что, чем шире спред, тем больше свобода выбора в значении цены опциона. Для российского рынка лучшая аппроксимация получалась у меня при выборе одинакового значения весов, равного 1, но я не брал в рассмотрение слишком дальние страйки.
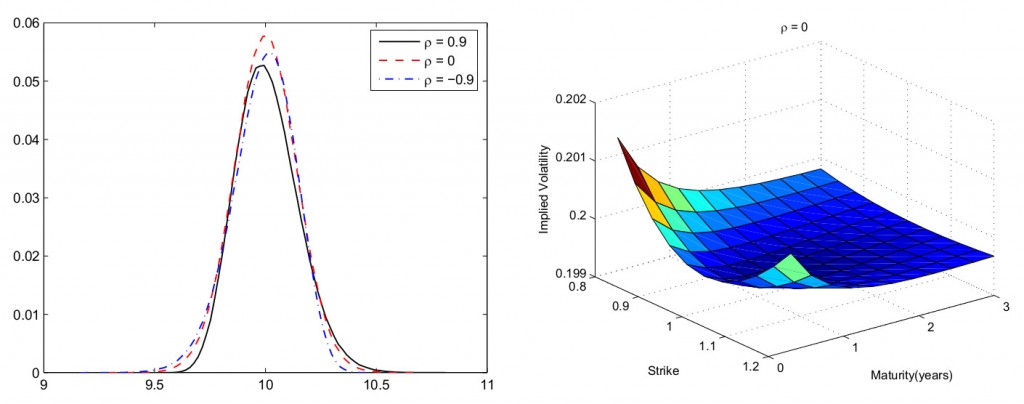
Получив параметры модели Хестона, мы сможем вычислить цены опционов 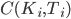 для любого страйка и периода до экспирации. Для наглядности мы сможем построить улыбку волатильности по значениям подразумеваемой волатильности из формулы Блэка-Шоулза, подставив в нее хестоновские цены опционов - см. график в начале поста.
для любого страйка и периода до экспирации. Для наглядности мы сможем построить улыбку волатильности по значениям подразумеваемой волатильности из формулы Блэка-Шоулза, подставив в нее хестоновские цены опционов - см. график в начале поста.
Модель Хестона отражает реальное статистическое распределение приращений цены базового актива значительно лучше, чем это делает модель Блэка-Шоулза, в чем вы сможете убедиться, сравнивая реальные рыночные цены опционов с полученными по этой модели. Однако у нее есть один существенный недостаток, который проявляется в том, что, если до экспирации остается небольшой срок (около недели для российского рынка) цены крайних страйков модель определяет неверно, в терминах подразумеваемой волатильности - хвосты улыбки начинают расходиться:
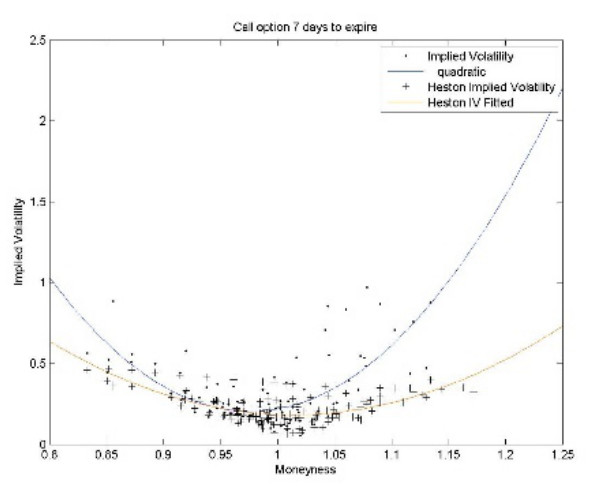 Чтобы устранить этот недостаток мы должны перейти к применению модифицированной модели Хестона - модели Бэйтса, являющейся одной из лучших аппроксимаций, позволяющих с макимальной точностью находить "справедливые" цены опционов. Ее мы рассмотрим в следующей части цикла статей про улыбку волатильности.
Чтобы устранить этот недостаток мы должны перейти к применению модифицированной модели Хестона - модели Бэйтса, являющейся одной из лучших аппроксимаций, позволяющих с макимальной точностью находить "справедливые" цены опционов. Ее мы рассмотрим в следующей части цикла статей про улыбку волатильности.
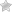


А как часто приходиться калибровать модель к рынку? И за какой период берутся рыночные цены? Имею ввиду вот это: <i>берем выборку цен для опционов разных страйков за определенный <b>период</b> времени</i>
Это зависит от вашей стратегии - ловите ли вы секундные отклонения, или работаете в большем масштабе времени. Все это подбирается при тестировании. Можно посоветовать одно - смотрите на волатильность базового актива, как она меняется, с какой амплитудой, скоростью. Отталкиваясь от этого, поймете. как выбрать период для ваших целей
Понял, спасибо.
А что можете сказать про "справедливость" рыночных цен (к которым калибруете модель)? Если предположить ситуацию, когда во всех стаканах (страйках) только один участник, он ведь может манипулировать улыбкой как угодно. Захотел в одну сторону загнул, захотел - в другую. Или ситуация, когда в стаканах вообще никого нет. Есть ли способ построить свою модель справедливых цен, вообще не заглядывая в текущие стаканы?
Такой способ есть, например модель локальной волатильности, которая использует параметры базового актива. Но насколько она будет соответствовать рынку, да еще при одном участнике, сложно сказать. Я пробовал строить такую модель, чисто теоретически, на практике не применял. Вроде что-то получалось, похожее на рыночные цены.
Поскольку есть история биржевой улыбки за несколько лет, то теоретически можно было бы проверить что точнее - рынок или модель.
А про тренды что думаете - бывают они, или движение цены состоит только из случайного блуждания + гэпы?
Интересный конечно вопрос. Я то внутри дня все смотрю, там устойчивые тренды - редкость. Поэтому даже не знаю что ответить. Случайное блуждание и гэпы - больше похоже на внутридневные движения
А если на горизонте неделя-месяц (до экспирации ближайшей серии)?
На такой длительности ценовые тренды несложно заметить, так что объективно они существуют. Только почему мы говорим о ценах, если торгуем волатильностью. Там тренды не нужны, нам нужен процесс возврата к среднему
Вот тут поспорю: имхо, торговля волатильностью - это только частный случай опционной торговли. Мне кажется, торговля опционами в общем случае - это торговля вероятностью. Вы же сами в этом и следующем посте (модель Бейтса) указываете, что цены опционов зависят от многих параметров, и волатильность (Vt) только один из них. Поэтому нас, по идее, должно интересовать все распределение вероятности целиком, а не только его второй момент (дисперсия, на нее влияет Vt). Наибольший вклад в распределение вносит именно первый момент.
В рыночном распределении первый момент должен равняться текущей цене БА. Но если бы научиться статистически значимо выделять иногда тренды, можно было бы строить распределение вероятностей на экспу более точное, чем рыночное. И таким образом получить преимущество перед рынком.
Вы скорее всего правы, я говорил только о своем опыте построения опционных стратегий. Сейчас я в основном занимаюсь линейными инструментами, нужно доделать то, что начал.
Кстати, по моим экспериментам, за эффект "толстых хвостов" отвечает не p (коэф-т корреляции), а сигма (волатильность волатильности). p отвечает за асимметрию распределения (и это видно на верхнем графике).
Возможно, спасибо за уточнение.
Вот просто ужасный код
// Функция суммирования элементов вектора
double VectorSum(double[] A)
{
double sum = 0;
double n = A.Length;
for (int i = 0; i <= n - 1; i++)
sum += A[i];
return sum;
}
Должно быть хотя бы хотя бы
double VectorSum(double[] A)
{
double sum = 0;
// -- и тип и дальнейшее сохранение проверки границ массива
// double n = A.Length;
for (int i = 0; i < A.Length; ++i)
sum += A[i];
return sum;
}
Гарантированно будет быстрее, может, даже больше чем на 50%.
А еще лучше через обращение по ссылке переписать до 70% будет веселее.
Но лучше этот блок или всю модель переписать в c++ и оттуда вызвать. Так как возможна векторизация цикла. Что добавит 2,8х - 3,5х ускорение.
День добрый, что-то смотрю я на код и много мыслей по микрооптимизациям возникает. Точно скажу, Можно существенно его разогнать. По крайней мере у меня стремление к онлайн алгоритмам.
1. Но перед этим хочется выдвинуть предположение о возможности факторизации. Или точнее рассмотреть вопрос, а существует ли возможность сжать сигнал на вход либо в форме разложения по главным компонентам, либо по главным компонентам ядра? Интуиция подсказывает, что да.
Смысл - ну раз так в 1000х и выше увеличить скорость моделирования. Еще не прибегая ни к какому GPGPU. По крайней мере из другого примера машина регрессии опорных векторов за 42 минуты (при чем с предкэшированием расчетов) и версия со снижением размерности - 1,5 секунды на аналогичной выборке, состоящей из 10,000 данных. Первая версия оставила 800 опорных векторов, вторая версия только 2 вектора и радиальная базисная функция.
Почему вопрос так стоит - нет осмысления модели и подтверждения экспериментом - пока недостаточно осознания. А многочисленные рассуждения на тему методов Монте-Карло сильно надоели.
2. Как вы решаете задачу в режиме реального времени?
3. Всегда изнутри подначивает вопрос - а не пробовали законы движения свои подставлять?
Ну вот пожалуй сам себе и отвечу.
Берем QuantLib и сходу в разделе примеров читаем различные траектории.
Разработчики QuantLib тоже не стесняются и многое базируют на Boost.
Ну и для информации - есть доказанные решения 1000х обгоняющие Монте-Карло, но я пока их у QuantLib не увидел. Им нужно в 20х меньше точек траекторий, соответственно, и время экономится.
Вот это уже ближе и лучше. А насчет Диф. Эволюции и ПСО - не совсем согласен. Будучи совмещенными с другими методами - они-то самые ударные.
Есть также книжечка с исходным кодом Heston Model in Mathlab and C#. Но там я не увидел быстрых траекторий.
Так что как говорил тов. Ленин учиться, учиться. А также бороться и искать.
Спасибо за поднятую тему.