В ряду алгоритмов, используемых в опционной торговле, значительное место занимают стратегии покупки/продажи волатильности. Смысл таких стратегий в покупке опциона, когда волатильность рынка мала, и соответственно, продаже, когда волатильность высока, при постоянном хэджировании базисным активом ( дельта позиции равна нулю).
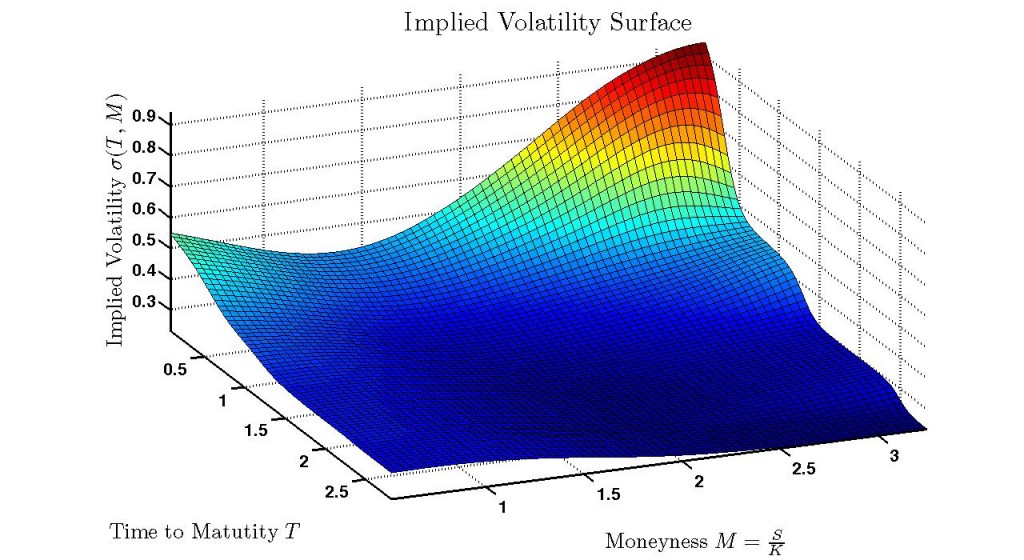
Цена опционов, как известно, вычисляется по формуле Блэка-Шоулза, однако из-за того, что некоторые допущения, относящиеся к модели цены базисного актива, не соответствуют реальному статистическому распределению, опционам разных страйков приходится присваивать различные значения так называемой подразумеваемой волатильности (IV), которая входит в уравнение Блэка-Шоулза как параметр. Возникает ситуация с двумя неизвестными - мы вычисляем IV по текущей цене опциона, при этом не зная, насколько справедлива эта цена в настоящий момент, следовательно не можем определить, дешево стоит опцион сейчас или дорого. Если бы нам удалось определить истинную волатильность рынка , то рассчитав по ней цену и сравнив с текущей, можно было бы принимать решение о покупке или продаже опциона. Поэтому основная задача, которую нужно решить в стратегиях покупки/продажи волатильности - построение правильного графика подразумеваемой волатильности опционов, в зависимости от страйков, из-за его формы имеющим название улыбки волатильности, или поверхности волатильности, если речь идет о разных периодах до экспирации - см. график в заглавии.
Необязательно идти именно таким путем - находить справедливую цену через подразумеваемую волатильность с помощью формулы Блэка-Шоулза. Можно, например, составить модель цены базисного актива, которая лучше подходит к реальному стат. распределению, и в результате непосредственно вычислить справедливую цену опциона, основываясь на наблюдаемых рыночных параметрах, исключая посредников, подобных IV. Так работают, например, модели Хестона и Бейтса, которые мы рассмотрим в следующих частях этого цикла статей. Но самый простой и очевидный вариант - все-таки использовать подразумеваемую волатильность из формулы БШ, применив технику ad-hoc Блэк-Шоулз - прикладного Блэка-Шоулза - для построения правильной улыбки волатильности. Эту технику мы и разберем подробно в этой части.
Напомним сначала саму формулу Блэка-Шоулза для колл опциона европейского типа:
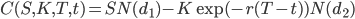
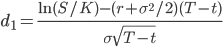
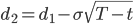
где С(S,K,T,t) - текущая стоимость опциона на момент времени t;
S - текущая цена базисного актива;
N(x) - интегральная функция нормального распределения;
К- страйк опциона;
r - безрисковая процентная ставка (для маржируемых опционов, торгуемых на бирже MOEX r=0);
T-t - время до экспирации;
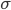 - подразумеваемая волатильность.
- подразумеваемая волатильность.
Формулу БШ можно записать в виде функции :
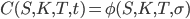 , (r сразу положим равной 0), Т обозначим время до экпирации.
, (r сразу положим равной 0), Т обозначим время до экпирации.
Тогда подразумеваемую волатильность можно найти с помощью обратной функции:
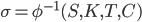
Для упрощения обозначим цены опционов как 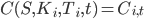 , где
, где 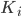 - цены страйков,
- цены страйков, 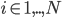 , N - количество страйков, для которых можно определить рыночную цену. Так как подразумеваемая волатильность будет разной для разных страйков и сроков до экспирации, можно записать формулу для нее следующим образом:
, N - количество страйков, для которых можно определить рыночную цену. Так как подразумеваемая волатильность будет разной для разных страйков и сроков до экспирации, можно записать формулу для нее следующим образом:
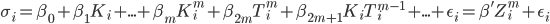
где 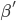 - вектор коэффициентов,
- вектор коэффициентов, 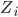 - вектор объясняющих переменных (страйки и время до экспирации),
- вектор объясняющих переменных (страйки и время до экспирации), 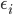 - вектор ошибок.
- вектор ошибок.
Наша задача - найти коэффициенты 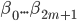 . Для этого сначала вычисляем подразумеваемые волатильности для всех страйков и сроков до экспирации из наблюдаемых рыночных цен за определенный период времени, затем с помощью метода наименьших квадратов находим коэффициенты
. Для этого сначала вычисляем подразумеваемые волатильности для всех страйков и сроков до экспирации из наблюдаемых рыночных цен за определенный период времени, затем с помощью метода наименьших квадратов находим коэффициенты 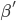 , минимизируя выражение:
, минимизируя выражение:
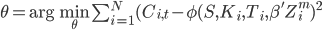
Число наблюдаемых точек N должно быть больше или равно 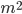 . Для практических целей, как правило, достаточно m=5.
. Для практических целей, как правило, достаточно m=5.
Итак, в результате мы можем найти "справедливые" цены для любого страйка и срока до экспирации, подставляя в формулу Блэка-Шоулза подразумеваемые волатильности, вычисленные через найденные коэффициенты 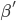 и значения этих страйков и периодов экспирации на текущий момент времени:
и значения этих страйков и периодов экспирации на текущий момент времени:
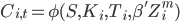
В помощь - примеры на языке C++ для вычисления цен опционов пут и колл и вычисление подразумеваемой волатильности из текущей рыночной цены опциона бисекционным методом:
// Формула Блэка-Шоулза
//здесь Т - время до экспирации,
//v - подразумеваемая волатильность
//PutCall - 'C' - вычисление цены для колл опциона, иначе - пут опцион
double BSPrice(double S, double K, double r, double T, double v, char PutCall) {
double d = (log(S/K) + T*(r + 0.5*v*v)) / (v*sqrt(T));
double Call = S*N(d) - exp(-r*T)*K*N(d - v*sqrt(T));
if (PutCall=='C')
return Call;
else
return Call - S + K*exp(-r * T);
}
// Вычисление подразумеваемой волатильности
//a - минимальное значение волатильности (например 0.00001)
//b - максимальное значение волатильности (например 10.0)
//MktPrice - рыночная цена опциона
double BisecBSV(double S, double K, double r, double T,
double a, double b, double MktPrice, char PutCall) {
const int MaxIter = 1000;
double Tol = 0.0000001;
double midP, midCdif;
double lowCdif = MktPrice - BSPrice(S, K, r, T, a, PutCall);
double highCdif = MktPrice - BSPrice(S, K, r, T, b, PutCall);
if (lowCdif*highCdif > 0) {
double Temp = lowCdif;
lowCdif = highCdif;
highCdif = Temp;
}
else
for (int i=0; i< =MaxIter; i++) {
midP = (a + b) / 2.0;
midCdif = MktPrice - BSPrice(S, K, r, T, midP, PutCall);
if (abs(midCdif)<Tol) goto LastLine;
else {
if (midCdif>0) a = midP;
else b = midP;
}
}
LastLine:
return midP;
}
В следующей части цикла будем находить справедливые цены опционов с помощью модели Хестона.


Привет, есть чудесная библиотека где все реализовано https://github.com/lballabio/quantlib
Круто!
А может быть такое (не судите строго я новичёк), что S и K у брокер одинаковый?
Не совсем понял вопрос. S - это цена базового актива, K- страйк, в какой -то момент они могут быть одинаковы. При чем здесь брокер?