Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии - наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
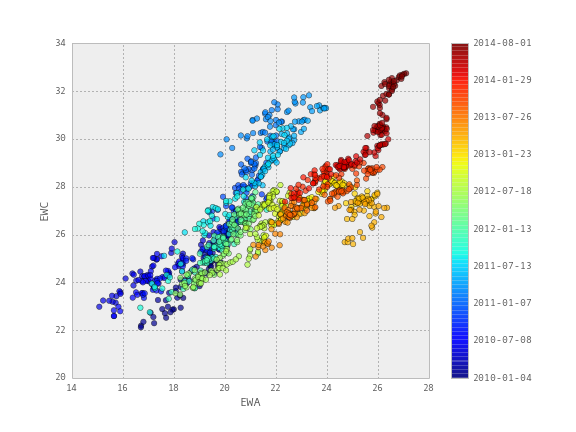
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF - австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
Приведем сначала уравнение линейной регрессии:
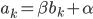 ,
,
где 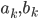 - приведенные цены фондов EWC и EWA соответственно, а
- приведенные цены фондов EWC и EWA соответственно, а 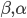 - коэффициенты регрессии - угол наклона и пересечение соответственно. Перепишем уравнение в матричной форме:
- коэффициенты регрессии - угол наклона и пересечение соответственно. Перепишем уравнение в матричной форме:
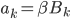 ,
,
![\beta=[\beta\;\alpha]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_74a042fcd6cb2d01a13521ef5d4b654a.gif)
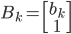
Фильтр Калмана - это модель пространства состояний, которая применяется рекурсивно на входном потоке зашумленных данных для получения статистически оптимальной оценки состояния системы. Общая форма фильтра Калмана содержит передаточное уравнение и уравнение наблюдений:
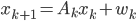
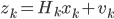
где 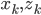 - вектор скрытых состояний и вектор наблюдений в момент времени k,
- вектор скрытых состояний и вектор наблюдений в момент времени k, 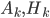 - матрица переходов и наблюдений соответственно,
- матрица переходов и наблюдений соответственно, 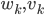 - векторы гауссовского шума с нулевым средним.
- векторы гауссовского шума с нулевым средним.
Для наших целей предположим, что вектор состояний 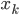 соостветствует вектору коэффициентов регрессии
соостветствует вектору коэффициентов регрессии 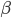 . Также предположим, что угол наклона и пересечение следуют процессу случайного блуждания (random walk), тогда
. Также предположим, что угол наклона и пересечение следуют процессу случайного блуждания (random walk), тогда 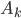 будет равна матрице идентичности
будет равна матрице идентичности 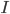 (матрице, где на главной диагонали единицы, остальные элементы - нули). В этом случае передаточное уравнение запишется:
(матрице, где на главной диагонали единицы, остальные элементы - нули). В этом случае передаточное уравнение запишется:
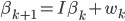 ,
,
то есть 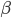 в следующий момент времени равна
в следующий момент времени равна 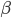 в текущий момент времени плюс шумовая составляющая.
в текущий момент времени плюс шумовая составляющая.
На следующем шаге применим нашу модель к уравнению наблюдений фильтра Калмана. Для этого приведенные цены закрытия актива EWC обозначим как вектор наблюдений 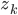 , и матрицу наблюдений
, и матрицу наблюдений 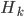 представим как вектор размерности 1х2 , содержащий в первой колонке приведенные цены закрытия EWA и единицами во второй колонке, подобно нашему вектору
представим как вектор размерности 1х2 , содержащий в первой колонке приведенные цены закрытия EWA и единицами во второй колонке, подобно нашему вектору 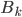 . Таким образом, это просто линейная регрессия между двумя активами. Для подпрограммы на Python - pykalman, конструирующей фильтр Калмана, матрица наблюдений obs_mat выглядит так:
. Таким образом, это просто линейная регрессия между двумя активами. Для подпрограммы на Python - pykalman, конструирующей фильтр Калмана, матрица наблюдений obs_mat выглядит так:
obs_mat = np.vstack([data.EWA, np.ones(data.EWA.shape)]).T[:, np.newaxis] array([[[ 19.36, 1. ]], [[ 19.42, 1. ]], [[ 19.49, 1. ]], ..., [[ 26.02, 1. ]], [[ 26.24, 1. ]], [[ 26.42, 1. ]]])
Последнее, что нужно сделать - определить шумовые составляющие 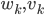 . Установим ковариацию наблюдений,
. Установим ковариацию наблюдений, 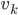 , как единичный вектор. Тогда будем трактовать ковариацию переходов,
, как единичный вектор. Тогда будем трактовать ковариацию переходов, 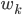 , как настраиваемый параметр для управления скоростью изменения коэффициентов регрессии:
, как настраиваемый параметр для управления скоростью изменения коэффициентов регрессии:
delta = 1e-5 trans_cov = delta / (1 - delta) * np.eye(2)
Далее установим класс фильтра Калмана KalmanFilter из модуля pykalman :
kf = KalmanFilter(n_dim_obs=1, n_dim_state=2, initial_state_mean=np.zeros(2), initial_state_covariance=np.ones((2, 2)), transition_matrices=np.eye(2), observation_matrices=obs_mat, observation_covariance=1.0, transition_covariance=trans_cov)
и вычислим средние значения и ковариацию состояний:
state_means, state_covs = kf.filter(data.EWC.values)
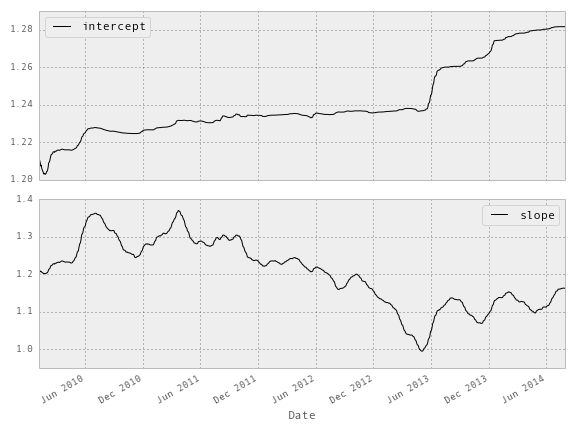
В итоге мы получаем графики изменений коэффициентов регресии - угла наклона (slope) и пересечения (intercept):
Более наглядно можно показать, как подстраиваются коэффициенты регрессии в течение времени на диаграмме рассеивания активов EWA и EWC: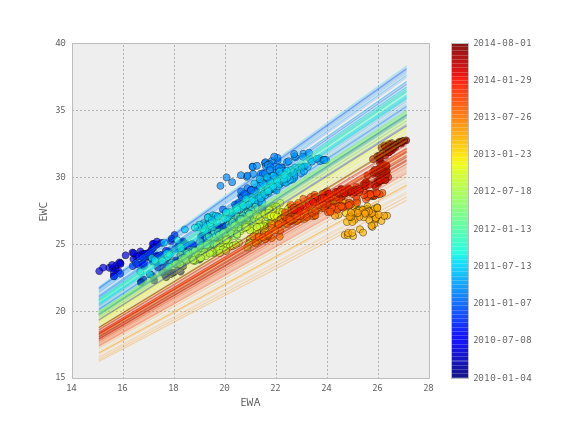
Думаю, те, кто практиковал парный трейдинг, найдет эту статью очень полезной, так как она решает один из главных вопросов в этом виде торговли - каким образом строить линейную регрессию, не попадая под обычную подгонку текущего состояния ценового спреда.



Сообщение