QuantAlgos

Перевод статьи из блога tr8dr, очень полезной для HFT трейдеров.

Алгоритмы высокочастотной торговли можно разделить на следующие категории:

1. Различные формы маркет мэйкинга (вероятно самый большой процент)

2.  Заработок на действиях других участников рынка или на микроструктуре рынка

3. Краткосрочный арбитраж

4. Алгоритмы исполнения больших заявок

Также среднесрочные стратегии подразделяются на:

1. Следование за трендом (если есть достаточно сильный импульс)

2. Следование за циклами (продажа/покупка в точках разворота высокоамплитудных ценовых циклов)

3. Долгосрочный арбитраж

Если сфокусироваться на алгоритмах маркет мэйкинга и следования тренду/циклам, то понимание ценового режима и ценовой функции очень важно.

Режим

Мы должны определять текущий ценовой режим для того, чтобы понимать, где мы можем применять стратегию маркет мэйкинга, а где следование тренду или циклам.

В частности, при маркет мэйкинге, могут быть периоды рыночной активности при которых такая стратегия может быть опасной ( то есть почти гарантировано будет терять деньги). Кроме очевидной опасности ценового гэпа из-за новостей или других событий, наибольшуую проблему создают периоды сильного импульса (momentum) на рынке. 

Возникает сильный перекос в исполнении ордеров, если рынок идет вверх (или вниз). Вы получаете сильный поток ордеров почти исключительно на покупку (продажу) и в результате остаетесь с короткой позицией на возрастающей (снижающейся) цене.

Таким образом, есть периоды в течение торгового дня, которые "хороши" для маркет мэйкинга ( т.е. когда поток ордеров сбалансирован и цена движется в ограниченном диапазоне), и периоды, когда лучше переключиться на импульсные стратегии, или стратегии для высокоамплитудных циклов.

Ценовая функция

Ценовая функция предоставляет нам ожидаемое среднее значение цены и его производные для некоторого периода в будущем, так же как и оценку шума и активности возврата к среднему. Эта информация неоценима в определении правильных цен для маркет мэйкинга при высокой волатильности цены.

Цели

Мы хотели бы иметь следующее:

1. Ценовую функцию с хорошим соответствием на предсказываемом интервале, привязанную к требованиям данного ценового режима

2. Понятие ценового режима

3. Другие метрики, такие как нижий и верхний пороги шума относительно ценовой функции (среднего значения), период и амплитуда сегментов момнотоного движения цены и т.п.

В контексте маркет мэйкинга мы ищем монотонную и почти линейную ценовую функцию, которая предоставит нам среднее значение в условиях ценового шума. Откалибровав фунцию подобным образом, мы получим удобное представление будущего значения цены и верхнюю и нижнюю границы ее возможных значений. Совместно с текущей открытой позицией это может быть использовано для подстройки рыночных ордеров.

В контексте импульса или циклов мы ищем ценовую функцию, которая будет следовать за импульсом или циклами с соответствующей кривизной и разумно предсказывающую (или следующую с низкой задержкой после) точки разворота цен.

Пример

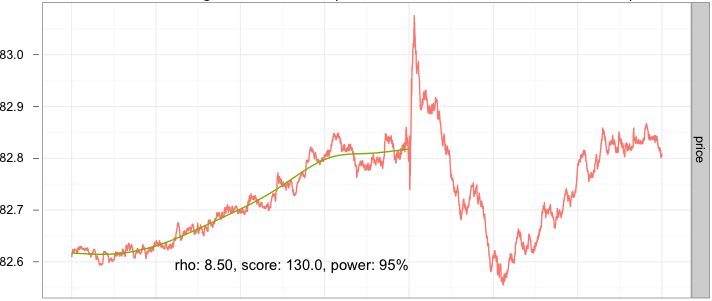
Приведем пример ценовой функции (зеленая линия на графике в заглавии) в период импульса ( в течение нескольких часов) встречающую нарушение и смену режима на циклический в определенный момент.

Далее идет продолжение этой ценовой серии с ценовой функцией для циклического режима:

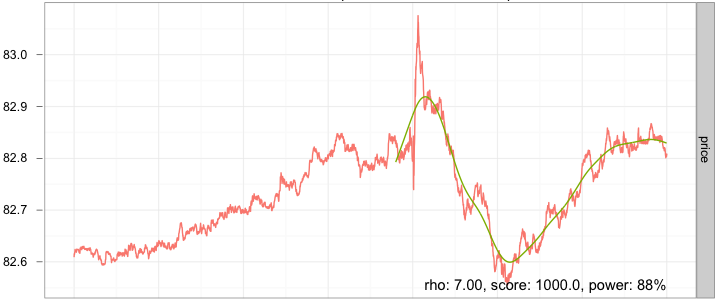Отметим, что вышеприведенная функция сглажена апостериори, так что траектория фильтра будет более зашумлена при сглаживании тик за тиком.

Эволюция подходов

Мы использовали множество подходов в прошлом для моделирования ценовой функции:

1. Различные фильтры из области обработки сигналов

2. Декомпозиция сигнала и затем его частичная реконструкция

3. Множество разных стохастических систем с фильтром Калмана

4. Прямая калибровка сплайнами по методу наименьших квадратов с различными эвристическими правилами

Наш текущий подход - это номер 4, но еще хотелось бы найти хорошее решение с использованием стохасических дифференциальных уравнений в байесовской среде, так как это более гибкий и элегантный способ. Наш последний опыт с фильтром Калмана столкнулся со сложностью в подборе параметров ( для состояний и измерения ковариаций) и функция быстро становилась нестабильной при возникновении неожиданных шумов.

 Продолжение следует.