QuantAlgos

Продолжение. Начало здесь.

Вы, наверное, заметили, что в процедуре вычисления параметров модели, описанной выше, я запоминал действительные предсказанные значения, так же как и предсказания направления приращения цены. Я хочу исследовать предсказательную способность величины  приращения. Точнее, может ли фильтрация сделок, в случаях, когда величина предсказанного приращения ниже определенного порога, улучшить доходность стратегии? Код ниже представляет такой анализ для небольших порогах приращений. Для упрощения, я конвертировал логарифмы приращений в простые приращения, чтобы получить управление знаком предсказания и облегчения применения порога:

# Test entering a trade only when prediction exceeds a threshold magnitude
simp.forecasts <- exp(ag.forecasts) - 1
threshold <- 0.000025
ag.threshold <- ifelse(simp.forecasts > threshold, 1, ifelse(simp.forecasts < -threshold, -1, 0))
ag.threshold.returns <- ag.threshold * returns[(window.length):length(returns)]
ag.threshold.returns[1] <- 0 # remove NA
ag.threshold.curve <- log(cumprod( 1 + ag.threshold.returns))
both.curves <- cbind(ag.threshold.curve, buy.hold.curve)
names(both.curves) <- c("Strategy returns", "Buy and hold returns")

# plot both curves together
plot(x = both.curves[,"Strategy returns"], xlab = "Time", ylab = "Cumulative Return",
     main = "Cumulative Returns",  major.ticks= "quarters", #
     minor.ticks = FALSE, ylim = c(-0.2, 0.45), col = "darkorange")
lines(x = both.curves[,"Buy and hold returns"], col = "blue")
legend(x = 'bottomleft', legend = c("Strategy", "B&H"),
       lty = 1, col = myColors)

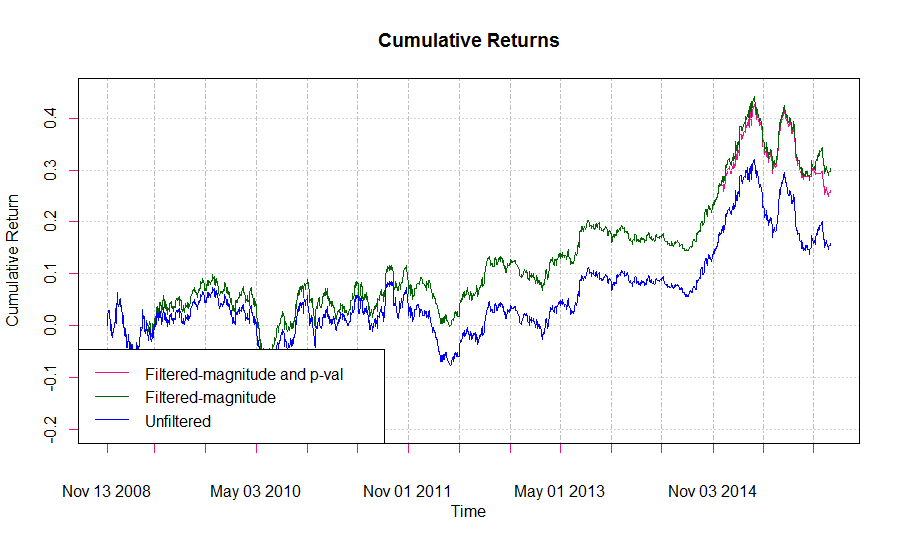
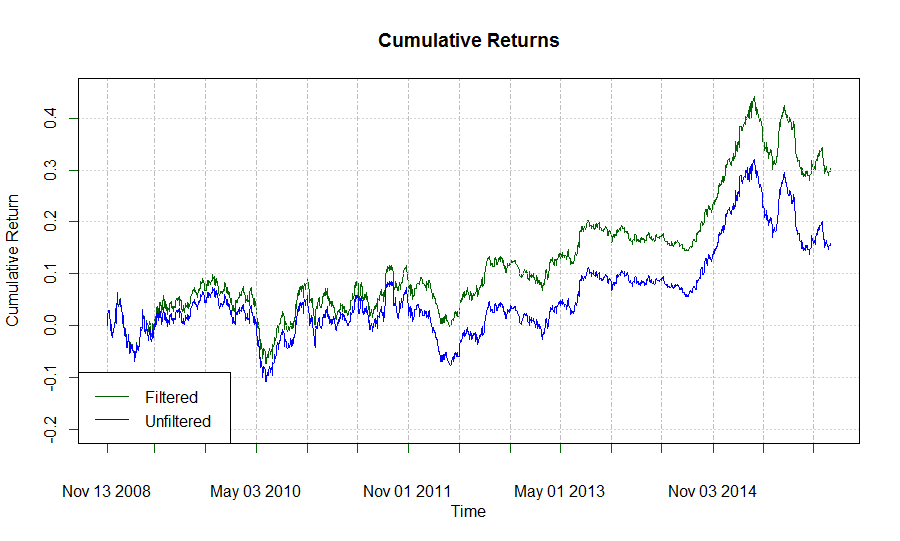
И такой результат получился по сравнению с первой стратегией:

    Похоже, что рассчитанная нами модель в некоторые дни может описывать лежащий в ее основе процесс лучше, чем в другие. Вероятно, если мы будем отфильтровывать сделки в тех случаях, где наша уверенность в точности модели меньше, то сможем повысить производительность стратегии. Такой подход требует вычисления статистической значимости ежедневного расчета модели, и вход в сделку должен осуществляться после того, как эта значимость превысит определенный порог.  Есть несколько путей достижения этой цели. Во-первых, мы можем визуально исследовать коррелограмму остатков модели и вынести суждение о том, насколько хорошо модель соответствует процессу. В идеале, остатки (шум) модели должны быть похожи на белый шум, то  есть серийная корреляция должна отсутствовать. Коррелограмма остатков может быть построена в R следующим образом:

acf(fit@fit$residuals, main = 'ACF of Model Residuals')

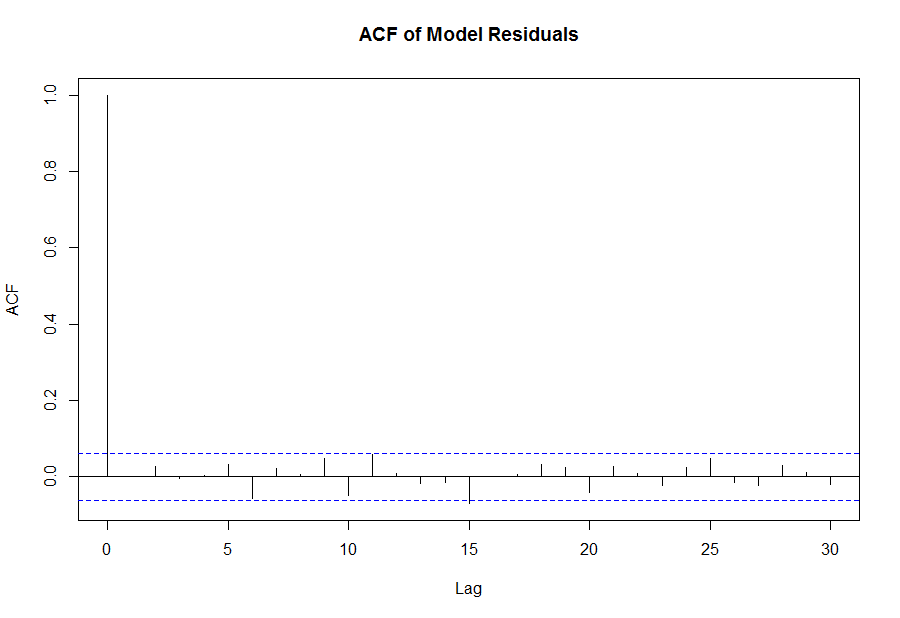Так как визуально эта коррелограмма представляет хорошее соответствие модели процессу, очевидно,что подход, основанный на субъективном суждении, не очень хорош. Лучший способ - проверить модель с помощью стаистики Льюнга-Бокса (Ljung-Box). Статистика Льюнга-Бокса - это проверка гипотезы о том, верно ли утверждение, что автокорреляция остатков вычисленной модели значительно отличается от 0. В этом тесте  нулевой гипотезой является предположение, что автокорреляция остатков равна 0, а альтернативой - то, что в процессе имеется серийная корреляция. Отклонение нулевой гипотезы и принятие альтернативы будет значить, что модель не очень хорошо подходит к процессу, так как есть необъясненные структуры в остатках. Статистика Льюнга-Бокса вычисляется в R следующим образом:

ljung.box <- Box.test(resid, lag = 20, type = "Ljung-Box", fitdf = 0)
ljung.box

Box-Ljung test

data: resid
X-squared = 23.099, df = 20, p-value = 0.284

В данном случае p-значение говорит о том, что остатки независимы и данная модель имеет хорошее соответствие процессу. Отметим, что статистика Льюнга-Бокса (величина X-squared в вышеприведенном коде) растет сильнее при увеличении автокорреляции остатков. Р-значение - это вероятность получения величины остатка такой же или более статистики при нулевой гипотезе. Таким образом, высокое р-значение является доказательством независимости остатков. Заметьте, что вычисление применяется для всех лагов, начиная с первого, что определено в функции Box.test().

Применяя тест Льюнга-Бокса к модели, пересчитываемой ежедневно, мы получаем очень мало дней, где отвергается нулевая гипотеза о независимости остатков, так что внедрив такой фильтр в нашу стратегию мы получим слабое соответствие модели и вряд ли это улучшит производительность, что и видно на графике в заглавии статьи.

Заключение и направления дальнейших исследований

Производительность стратегии ARMA/GARCH превышает доходность стратегии "купил и держи" на тестируемом периоде пары EUR/USD, хотя и не является слишком впечатляющей. Возможно улучшение доходности стратегии путем фильтрации по таким характеристикам, как величина предсказанного приращения и степень соответствия модели процессу, хотя последнее и не добавило много к конкретному алгоритму. Дополнительным фильтром может служить вычисление 95% доверительного интервала для ежедневного предсказания, и входить в сделку в том случае, если знаки каждого из порогов этого интервала совпадают, хотя это и может значительно уменьшить число сделок.

Есть очень много вариантов модели GARCH, например, экспоненциальная, интегральная, квадратичная, структурная и т.д. Они могут дать лучшее соответствие рассматриваемому процессу, чем простая модель GARCH(1,1), примененная в нашем примере. 

Я нахожу очень интересной область исследований, в которой предсказание временной серии осуществляется в результате сложной комбинации различных моделей,  например, взятием средней от индивидуального предсказания каждой модели, или поиском консенсуса, или большинством голосов о знаке предсказания. Заимствуя термин из машинного обучения, "ансамбль" моделей может часто генерировать более точное предсказание, чем  любая из его составляющих. Возможно полезным подходом будет совмещение предсказаний ARIMA/GARCH модели, представленной здесь, с обученной нейронной сетью или другим обучающимся методом.  Мы можем предположить, что ARIMA/GARCH модель объясняет линейные зависимости во временной серии, а нейронная сеть может хорошо  поймать зависимости нелинейные.