QuantAlgos

Статья из блога Robot Wealth.

Продолжая мои исследования в области моделирования временных серий, я решил изучить авторегрессивные и условные гетероскедатичные модели. В частности, я взял авторегрессивную модель ARIMA и общую авторегрессивную гетероскедатичную модель GARCH, так как на них часто сылаются в финансовой литературе. Далее следует описание того, что я узнал об этих моделях и основной процесс нахождения их параметров, а также простая торговая стратегия, основанная на предсказаниях полученной модели.

Сначала дадим несколько необходимых определений. Я не хочу воспроизводить всю теорию целиком, ниже дан краткий обзор моделирования временных серий, в частности ARIMA и GARCH моделей:

В первую очередь, вычисление ARIMA и GARCH моделей это способ узнать, при каких прошлых наблюдениях, шуме и дисперсии временной серии возможно предсказать следующее значения этой серии. Такие модели, параметры которых правильно установлены, имеют некоторую предсказательную способность, предполагая, конечно, что эти параметры остаются постоянными на некоторое время для данного процесса.

ARMA модель (пока без "I") - это линейная комбинация авторегрессивной (AR) модели  и скользящего среднего (МА). В AR модели предиктором является прошлое значении серии. МА модель структурно схожа с AR моделью, исключая предикторы для шума. Авторегрессивная модель со скользящей средней порядка p,q - ARMA(p,q) - это линейная комбинация упомянутых моделей и определяется как:

где  - белый шум и ,  - коэффициенты модели.

ARIMA (p,d,q) модель - это просто ARMA  модель, дифференцированная d раз - для получения стационарных серий.

GARCH модель также пытается объяснить гетероскедатичное поведение временной серии ( это характеристика кластерности волатильности) влиянием предыдущих значений серии (описываемых компонентом AR) и белым шумом (описваемым МА компонентом). GARCH модель использует авторегрессивный процесс для дисперсии, то есть использует прошлые значения дисперсии для вычисления будущих значений диспесии этой временной серии.

Далее, в рамках представленного контекста, я найду  ARIMA/GARCH модель для EUR/USD пары, и использую ее в качестве основы для торговой стратегии. Параметры модели вычисляются для каждого дня с применением процедуры подгонки, эта модель затем используется для предсказания приращения следующего торгового дня и соответственного вхождения в позицию, которая сохраняется в течение дня. Если предсказание совпадает с предсказанием предыдущего дня, существующая позиция сохраняется.

Скользящее окно логарифма приращений используется для вычисления параметров оптимальной модели ARIMA/GARCH на закрытии каждого торгового дня. Процедура подгонки основана на поиске параметров, которые минимизируют AIC ( информационный критерий Аикаке), но могут быть также применены и другие методы. Например, мы можем выбрать параметры, минимизирующие BIC (байесовский иформационный критерий), который может помочь уменьшить переподгонку в сложных моделях (то есть моделях с большим числом параметров). Такая процедура нахождения параметров была предложена Michael Halls-Moore  в посте ARIMA+GARCH trading strategy for the S&P500, и я одолжил у него часть кода.

Я выбрал скользящее окно размером 1000 дней для вычисления модели, но это значение является параметром для оптимизации. Можно взять столько данных, сколько возможно, для скользящего окна, но это может быть не оптимально для установления параметров модели для быстро меняющегося рынка. Я не буду проводить много экспериментов, но было бы интересно иследовать зависимость прибыльности модели от размеров скользящего окна. Далее код на языке R:

### ARIMA/GARCH trading model
library(quantmod)
library(timeSeries)
library(rugarch)

# get data and initialize objects to hold forecasts
EURUSD <- read.csv('EURUSD.csv', header = T)
EURUSD[, 1] < - as.Date(as.character(EURUSD[, 1]), format="%d/%m/%Y")
returns <- diff(log(EURUSD$C)) ## ttr::ROC can also be used: calculates log returns by default
window.length <- 1000
forecasts.length <- length(returns) - window.length
forecasts <- vector(mode="numeric", length=forecasts.length) 
directions <- vector(mode="numeric", length=forecasts.length) 
p.val <- vector(mode="numeric", length=forecasts.length) 

# loop through every trading day, estimate optimal model parameters from rolling window
# and predict next day's return
for (i in 0:forecasts.length) {
  roll.returns <- returns[(1+i):(window.length + i)] # create rolling window
  final.aic <- Inf
  final.order <- c(0,0,0)
  # estimate optimal ARIMA model order
  for (p in 0:5) for (q in 0:5) { # limit possible order to p,q <= 5
    if (p == 0 && q == 0) next # p and q can't both be zero
    arimaFit <- tryCatch( arima(roll.returns, order = c(p,0,q)), 
                          error = function( err ) FALSE,
                          warning = function( err ) FALSE )
    if (!is.logical( arimaFit)) {
      current.aic <- AIC(arimaFit)
      if (current.aic < final.aic) { # retain order if AIC is reduced
        final.aic <- current.aic
        final.order <- c(p,0,q)
        final.arima <- arima(roll.returns, order = final.order)
      }
    }
    else next 
  }

  # specify and fit the GARCH model
  spec = ugarchspec(variance.model <- list(garchOrder=c(1,1)),
                    mean.model <- list(
                      armaOrder <- c(final.order[1], final.order[3]), include.mean = T),
                    distribution.model = "sged")
  fit = tryCatch(ugarchfit(spec, roll.returns, solver = 'hybrid'), error = function(e) e, warning = function(w) w)
  
  # calculate next day prediction from fitted mode
  # model does not always converge - assign value of 0 to prediction and p.val in this case
  if (is(fit, "warning")) {
    forecasts[i+1] <- 0 
    print(0)
    p.val[i+1] <- 0
  }
  else {
    next.day.fore = ugarchforecast(fit, n.ahead = 1)
    x = next.day.fore@forecast$seriesFor
    directions[i+1] <- ifelse(x[1] > 0, 1, -1) # directional prediction only
    forecasts[i+1] <- x[1] # actual value of forecast
    print(forecasts[i])
    # analysis of residuals
    resid <- as.numeric(residuals(fit, standardize = TRUE))
    ljung.box <- Box.test(resid, lag = 20, type = "Ljung-Box", fitdf = 0)
    p.val[i+1] <- ljung.box$p.value
  }
}

dates <- EURUSD[, 1] 
forecasts.ts <- xts(forecasts, dates[(window.length):length(returns)])
# create lagged series of forecasts and sign of forecast
ag.forecasts <- Lag(forecasts.ts, 1)
ag.direction <- ifelse(ag.forecasts > 0, 1, ifelse(ag.forecasts < 0, -1, 0))

# Create the ARIMA/GARCH returns for the directional system
ag.direction.returns <- ag.direction * returns[(window.length):length(returns)]
ag.direction.returns[1] <- 0 # remove NA

# Create the backtests for ARIMA/GARCH and Buy & Hold
ag.curve <- log( cumprod( 1 + ag.direction.returns) )
buy.hold.ts <- xts(returns[(window.length):length(returns)], dates[(window.length):length(returns)])
buy.hold.curve <- log(cumprod(1 + buy.hold.ts))
both.curves <- cbind(ag.curve, buy.hold.curve)
names(both.curves) <- c("Strategy returns", "Buy and hold returns")

# plot both curves together
myColors <- c( "darkorange", "blue") 
plot(x = both.curves[,"Strategy returns"], xlab = "Time", ylab = "Cumulative Return",
     main = "Cumulative Returns", ylim = c(-0.25, 0.4), major.ticks= "quarters",
     minor.ticks = FALSE, col = "darkorange")
lines(x = both.curves[,"Buy and hold returns"], col = "blue")
legend(x = 'bottomleft', legend = c("Strategy", "B&H"),
       lty = 1, col = myColors)

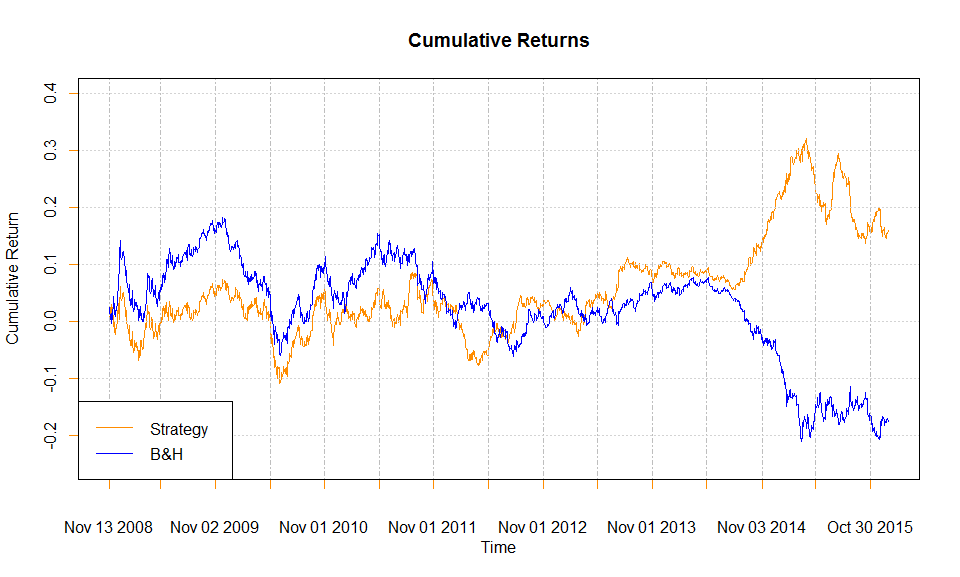
Предсказания получаются только для направления: покупаем, когда предсказано положительное приращения и продаем, когда отрицательное. Результат такого подхода в сравнении со стратегией "купил и держи" показано на рисунке в заглавии статьи.

Продолжение следует...