Еще одна статья с ресурса www.talaikis.com по разработке простой стратегии на модели Маркова с использованием Python.
Модель скрытых состояний Маркова - это производительная, вероятностная модель, в которой последовательность наблюдаемых переменных генерируется некоторыми неизвестными (скрытыми) состояниями. Мы попытаемся найти такие неизвестные вероятностные функции для, скажем, S&P500. Все опишем кратко, без проверок на ошибки, без тестов вне выборки и т.д. Мы делаем это для того, чтобы минимизировать склонность к ненужному усложнению для начинающих.
Что будем использовать:
библиотеку Python - hmmlearn.
1. Данные. Возьмем данные по свечам (OHLC), включающие объем, из нашей базы MongoDb :
data = read_mongo(dbase, symbl).pct_change().dropna() X = data.as_matrix() dates = data.index
2. Модель. Будем использовать гауссовскую модель НММ, хотя, вероятно, это не соответствует реальности (данные не подчиняются нормальному закону распределения), чтобы это компенсировать, зададим 8 скрытых состояний:
import pandas as pd from hmmlearn.hmm import GaussianHMM model = GaussianHMM(n_components=8, covariance_type="diag", n_iter=1000).fit(X) # предсказание оптимальной последовательности по внутреннему скрытому состоянию hidden_states = model.predict(X)
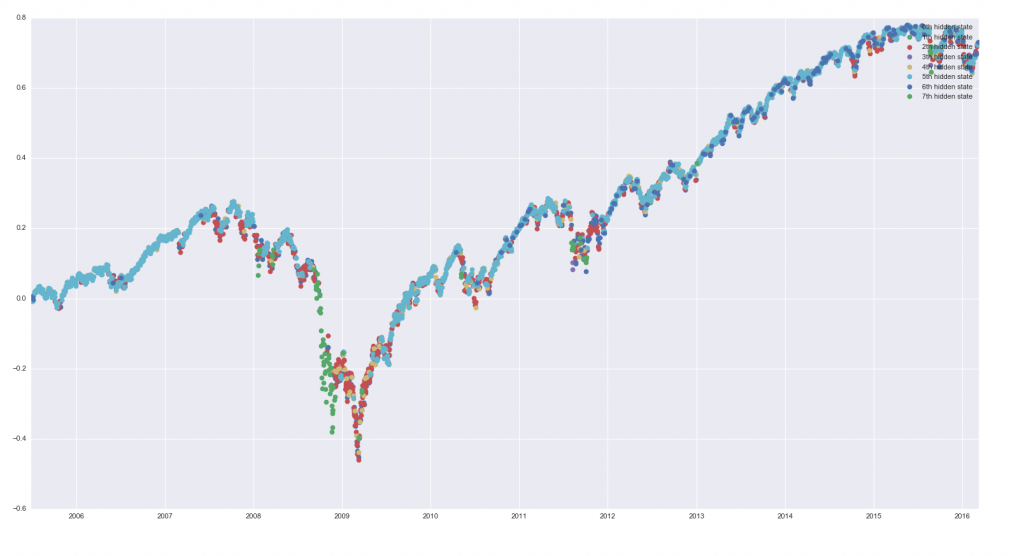
3. Скрытые состояния на графике показаны в заглавии статьи:
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
for i in range(model.n_components):
idx = (hidden_states == i)
plt.plot_date(dates[idx], data.CLOSE.cumsum()[idx], 'o', label="%dth hidden state" %i, lw=1)
plt.legend()
plt.grid(True)
plt.show()
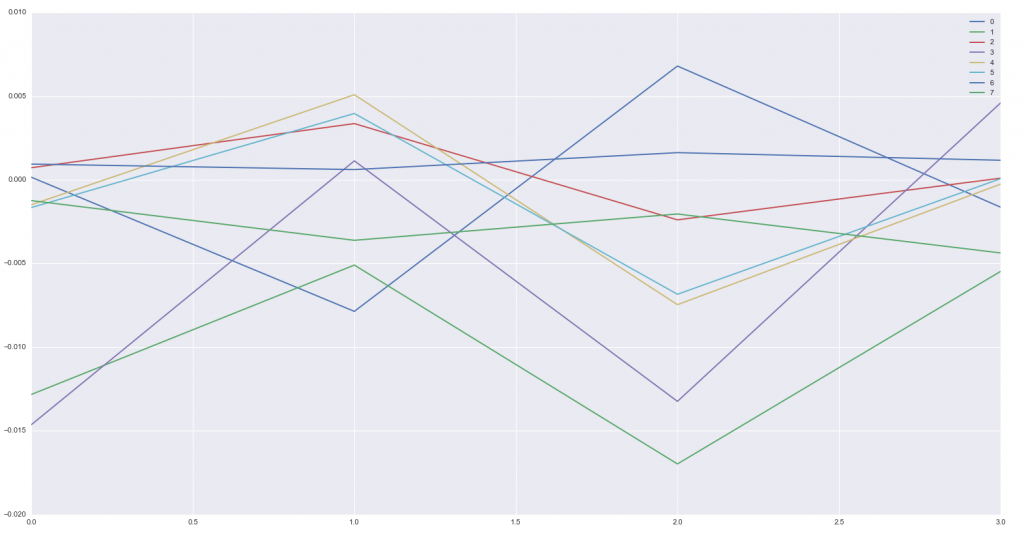
4. Составим статистику по этим генерирующим процессам:
print "Среднее и его изменение по каждому скрытому состоянию"
for i in range(model.n_components):
print "%dth hidden state" %i
print "mean = ", model.means_[i]
print "var = ", np.diag(model.covars_[i])
#plt.plot(pd.DataFrame(np.diag(model.covars_[i]))[:-1], label=i)
plt.plot(pd.DataFrame(model.means_[i])[:-1], label=i)
plt.legend()
plt.show()
Мы можем увидеть здесь наши паттерны. Наиболее интересный - очень стабильное положительное среднее.
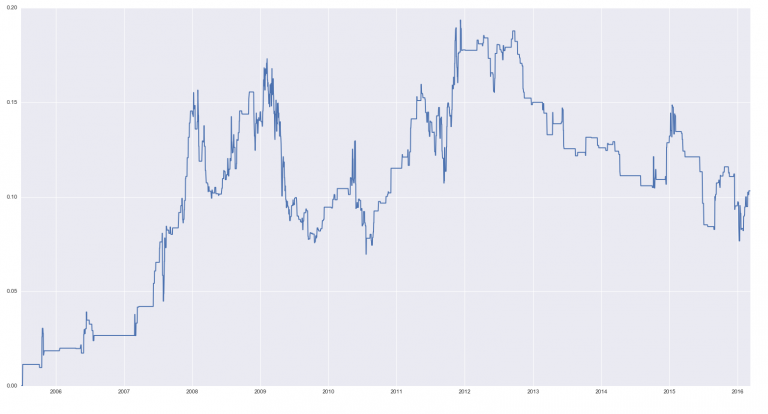
5. Каждое состояние (фактор) в вероятно самом коротком в мире бэктесте:
for i in range(model.n_components):
idx = (hidden_states == i)
#быстрое тестирование каждого фактора
df = data.CLOSE
data['sig_ret%s'%i] = df.multiply(idx, axis=0)
plt.plot(data['sig_ret%s'%i].cumsum())
plt.show()
НММ0, скорее всего, фактор высокой волатильности:
НММ1, НММ3 очень редкие, в основном на медвежьих рыночных выбросах. НММ7 один из двух процессов волатильности, но относительно редкий.
НММ2 очень интересный, потому что начал работать в 2012 году:
НММ4, НММ5 - медвежьи процессы, ясно видимые на графиках средних (см. выше):
НММ6 - бычий процесс, также видимый на графике средних, как очень стабильное среднее:
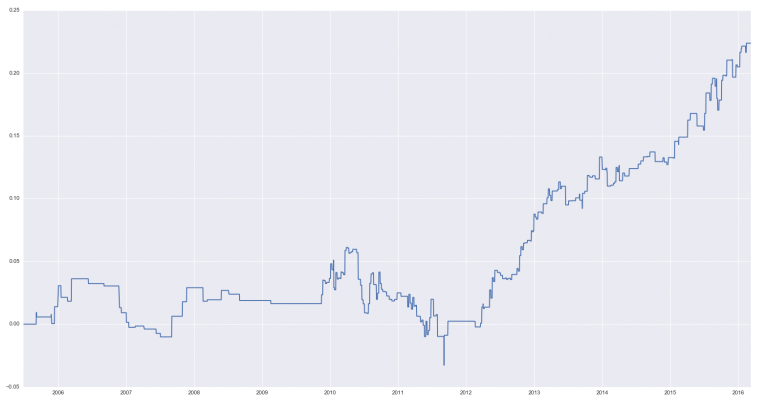
6. Проверим, сможем ли мы торговать эти компоненты, покупать НММ7 и продавать НММ4 и 5, игнорируя другие состояния;
mts = data['sig_ret7'] - data['sig_ret4'] - data['sig_ret5'] plt.plot(mts.cumsum()) plt.show()
Мы проделали много работы здесь, можно на этом закончить.
P.S. Более реалистичный пример на выборке "in-sample" с нормализованными данными, 2 состояния и 1 день задержки по сигналу. Сравнение со стратегией "купил и держи" (зеленая линия):

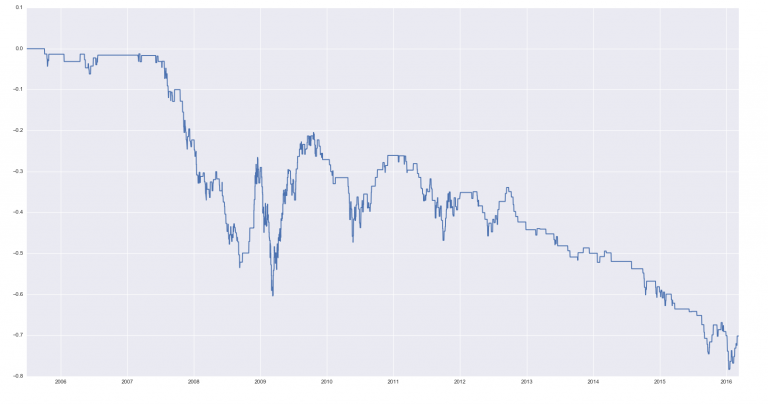
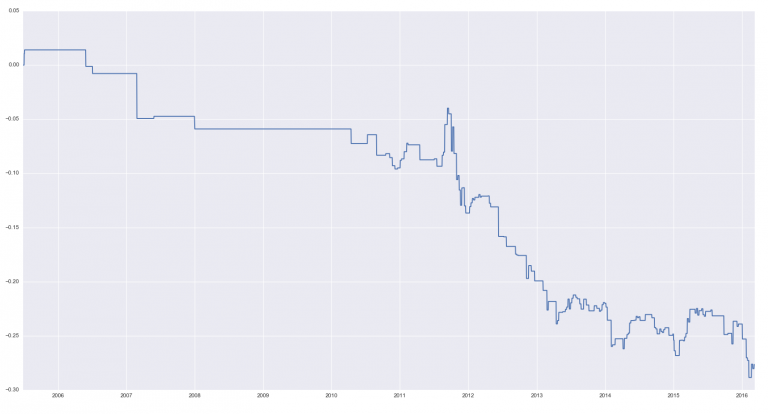
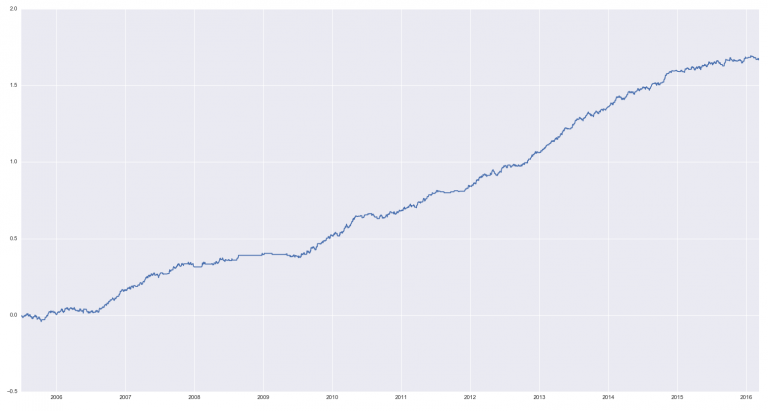
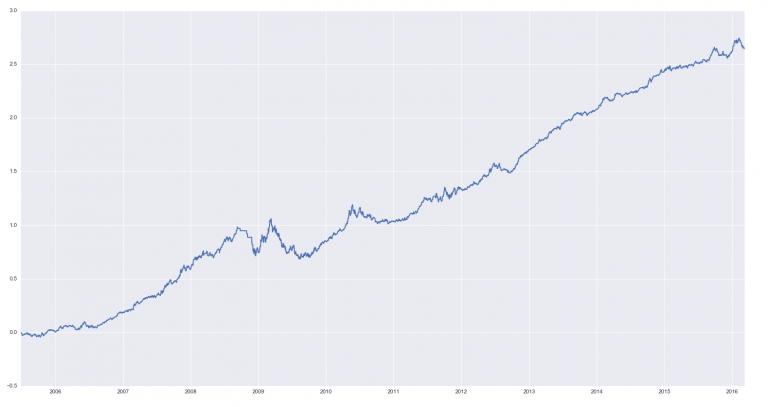
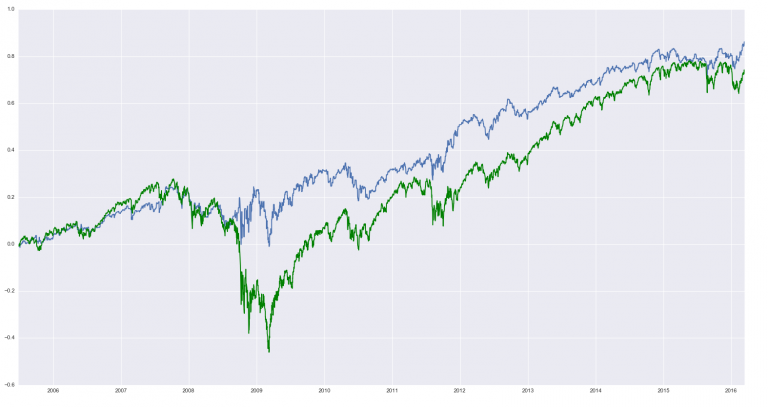


Я бы хотел предостеречь тех, кто будет использовать результаты predict() этой модели. Она расставляет скрытые состояния "задним числом". Это легко проверить, если сравнить предсказанные состояния (пусть их будет 2) и реальные последние, если идти по наблюдениям окном и брать последнее предсказанное состояние.
Первая колонка - predict() на out of sample. Вторая колонка - что получается, если мы не знаем будущего.
Хорошо видно, что метод predict заглядывает в будущее на один шаг.
0 0
0 0
1 0
1 1
1 1
1 0
1 1
1 1
1 1
1 1
0 1
0 0
0 0