Небольшая статья с ресурса http://www.talaikis.com/ о построении простой стратегии, использующую наивный байесовский классификатор при создании процесса возврата к среднему. Весь код в статье приведен на языке Python.
Это достаточно большая область исследований, но расскажем все очень кратко. Мы попытаемся найти взаимоотношение между временными сериями (в данном случае возьмем в качестве сигнала взаимный фонд XLF из финансового сектора, сдвинутый по времени на 1 день назад), а нашей целью будет фьючерс S&P500 в форме CFD. Будем входить в длинную позицию по этой бумаге при нулевой вероятности приращения. Логически нулевая вероятность ни о чем не говорит, другими словами, будем покупать возврат к среднему.
1. Получение данных
Y = read_mongo(dbase, "S&P5001440") X = read_mongo(dbase, syms[s]).shift() #готовим набор данных res = pd.concat([X.CLOSE, Y.CLOSE], axis=1, join_axes=[X.index]).pct_change().dropna() res.columns = ['X', 'Y']
2. Далее мы конструируем матрицу ошибок.Если сигнал растет и S&P500 растет - это истинное положительное значение, если сигнал вверх, а S&P500 -вниз, это ложное положительное значение, то же для отрицательных сигналов. Мы делаем это двумя способами:
#матрица ошибок res['true_positive'] = np.where(np.where((res['X'] > 0), res['Y'], 0) > 0, res['Y'], 0) res['false_positive'] = np.where((np.where((res['X'] > 0), res['Y'], 0) < 0), res['Y'], 0) res['true_negative'] = np.where((res['X'] < 0) & (res['Y'] < 0), res['Y'], 0) res['false_negative'] = np.where((res['X'] < 0) & (res['Y'] > 0), res['Y'], 0)
3. Преобразуем сигналы в булевы переменные, используя скользящую сумму из 10 значений по всем сигналам:
#скользящая сумма сигналов w = 10 res['true_positive_sum'] = pd.rolling_sum(res['true_positive'].astype(bool), window=w) res['false_positive_sum'] = pd.rolling_sum(res['false_positive'].astype(bool), window=w) res['true_negative_sum'] = pd.rolling_sum(res['true_negative'].astype(bool), window=w) res['false_negative_sum'] = pd.rolling_sum(res['false_negative'].astype(bool), window=w)
4. Теперь попытаемся определить вероятность сигналов обоих направлений. Для этого используем простую формулу частот:
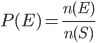
смысл которой в том, что вероятность события равна числу желаемых событий , деленных на число всех возможных событий:
res['accuracy'] = (res['true_positive_sum'] + res['true_negative_sum']) / (res['true_positive_sum'] + \
res['true_negative_sum'] + res['false_positive_sum'] + res['false_negative_sum'])
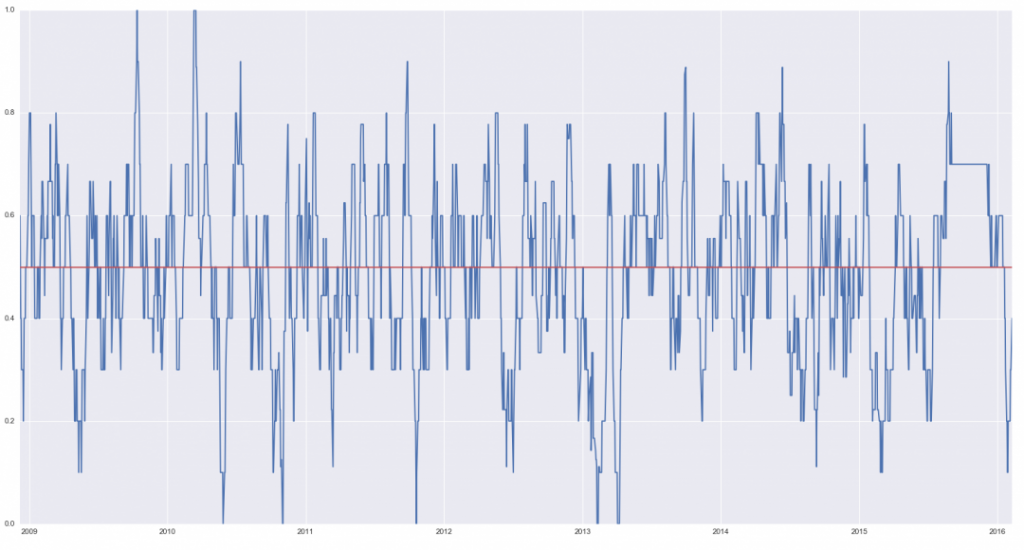
plt.plot(res['accuracy'])
plt.axhline(0.5, color = 'r', xmax=5)
plt.show()
5. Вычислим вероятности противоположных событий:
res['true_positive_ratio'] = res['true_positive_sum'] /(res['true_positive_sum'] + res['false_negative_sum']) res['false_positive_ratio'] = res['false_positive_sum'] / (res['false_positive_sum'] + res['true_negative_sum']) res['true_negative_ratio'] = 1 - res['true_positive_ratio'] res['false_negative_ratio'] = 1 - res['false_positive_ratio']
6. Сейчас мы можем вычислить сигналы и прибыльность. Будем использовать десятикратное плечо при расчете прибыли. Код ниже дан для ситуации " вход в лонг при отрицательной вероятности":
res['signal'] = np.where(res['true_negative_ratio'] >= 1, 1, 0) res['returns'] = res['signal'].shift() * res['Y'] * 10.0
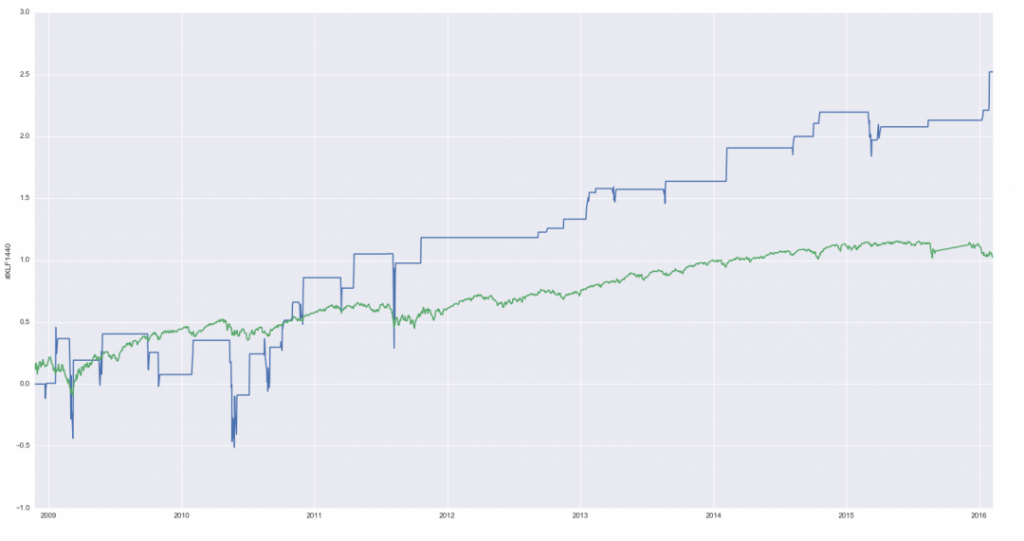
В заглавии статьи показан график кумулятивной прибыли по сравнению со стратегией "купил и держи" ( линия зеленого цвета).
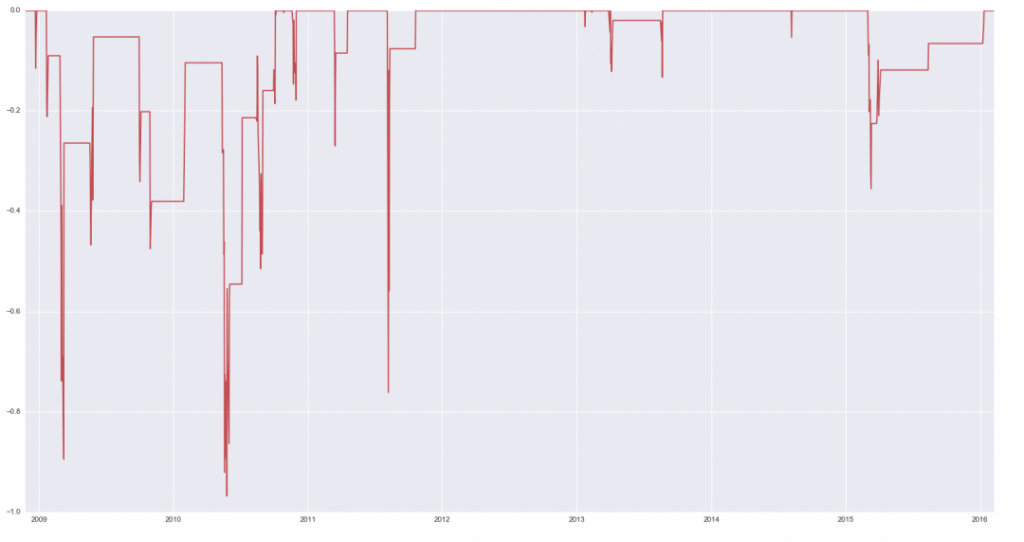
Ниже - график просадок:
Конечно, векторизованный бэктест показывает только, как это было бы при входе и выходе на закрытии дня, не учитывает комиссий и т.п.



Хорошая демонстрация чистого мышления.
Однако как обычно у любителей классификации очень сложно оценить ожидаемый доход.