Начало здесь.
Зависит ли корреляция сигналов от оборачиваемости?
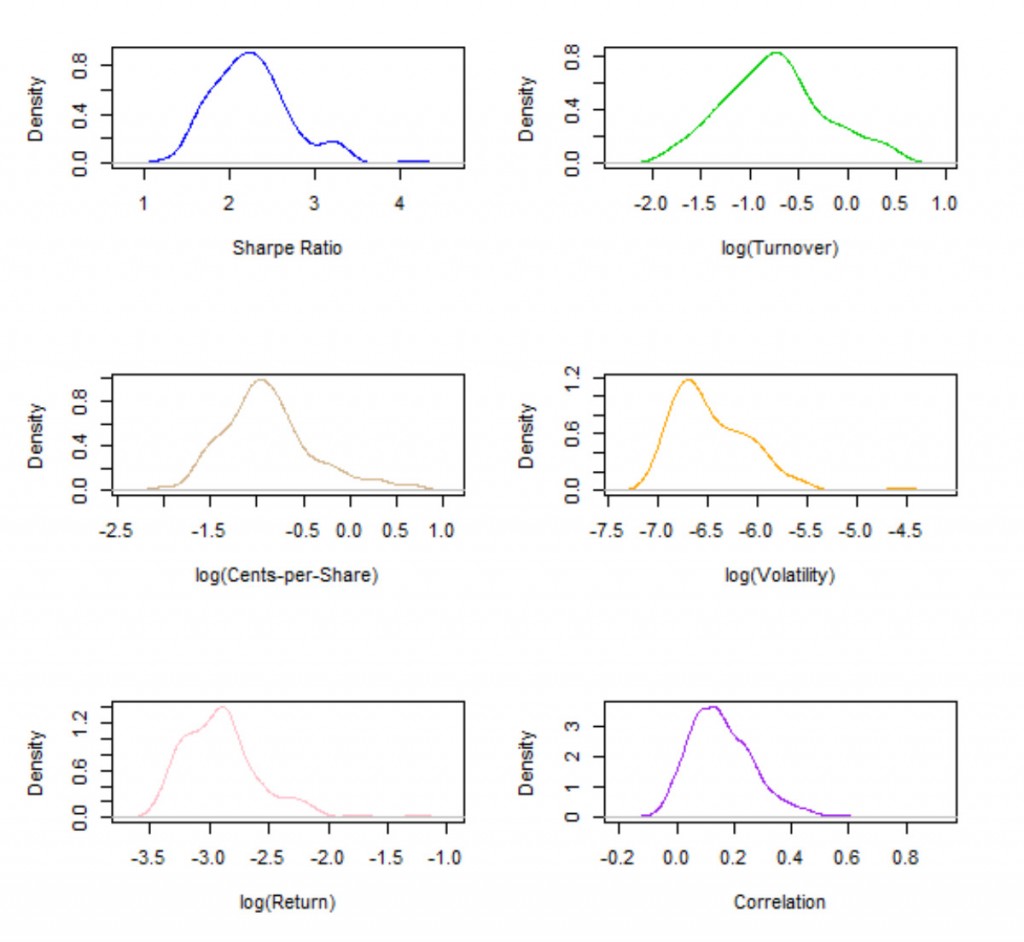
Если мы проведем параллель между сигналами и акциями, то оборачиваемость по каждому альфа-сигналу является аналогом ликвидности акций, которая обычно измеряется через средний дневной объем торгов (ADDV). Логарифм ADDV обычно используется как фактор риска в многофакторных моделях для аппроксимации ковариации матричной структуры портфеля ценных бумаг, чье назначение заключается в моделировании вне-диагональных элементов ковариационной матрицы, то есть структуры парных корреляций. Следуя этой аналогии, мы можем задать вопрос, может ли оборачиваемость – или точнее ее логарифм – объяснить корреляции альфа-сигналов? Очевидно, что примененение оборачиваемости напрямую (в отличие от логарифма) ничего не даст из-за чрезвычайно искаженного (грубо логарифмически нормального) распределения оборота (см. рисунок в заглавии).
Чтобы ответить вопрос в заголовке, вспомним, что в факторной модели ковариационная матрица моделируется как:
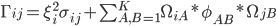
Здесь 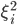 - отдельная мера риска,
- отдельная мера риска, 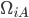 - это матрица факторов размерностью NxK, соответствующая K<<N факторам, и
- это матрица факторов размерностью NxK, соответствующая K<<N факторам, и 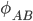 - ковариационная матрица факторов. В нашем случае, мы заинтересованы в моделировании корреляционной матрицы
- ковариационная матрица факторов. В нашем случае, мы заинтересованы в моделировании корреляционной матрицы 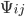 , и в доказательствах, что оборачиваемость может объяснять попарную корреляцию. Отдельной темой также является корреляция между оборачиваемостью и волатильностью.
, и в доказательствах, что оборачиваемость может объяснять попарную корреляцию. Отдельной темой также является корреляция между оборачиваемостью и волатильностью.
Наш подход состоит в представлении одного из столбцов матрицы факторов, как 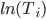 . Точнее, заранее нет никакой причины, почему мы должны выбрать
. Точнее, заранее нет никакой причины, почему мы должны выбрать 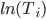 в противоположность к
в противоположность к 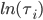 , где
, где 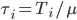 , и
, и 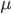 - некоторый коэффициент нормализации. Чтобы разобраться с этим, нормализуем
- некоторый коэффициент нормализации. Чтобы разобраться с этим, нормализуем 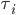 так, что функция
так, что функция 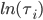 будет иметь нулевую кросс-секционную среднюю , и пусть
будет иметь нулевую кросс-секционную среднюю , и пусть 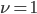 будет единичным вектором. Затем мы можем построить три симметричных тензорных комбинации
будет единичным вектором. Затем мы можем построить три симметричных тензорных комбинации 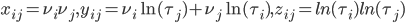 . Cейчас определим сводный индекс
. Cейчас определим сводный индекс 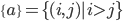 , который принимает M = (N − 1)/2 значений, то есть мы преобразуем элементы нижнего треугольника основной симметричной матрицы
, который принимает M = (N − 1)/2 значений, то есть мы преобразуем элементы нижнего треугольника основной симметричной матрицы 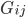 в вектор
в вектор 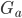 . Таким образом мы можем создать четыре М-вектора
. Таким образом мы можем создать четыре М-вектора 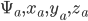 . Тогда можно запустить линейную регрессию
. Тогда можно запустить линейную регрессию 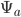 по
по 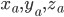 . Отметим, что
. Отметим, что 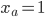 - просто единичный вектор, таким образом получается регрессия
- просто единичный вектор, таким образом получается регрессия 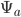 по
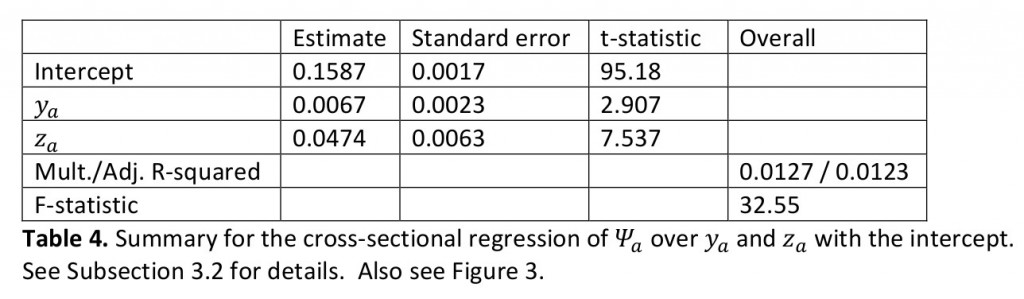
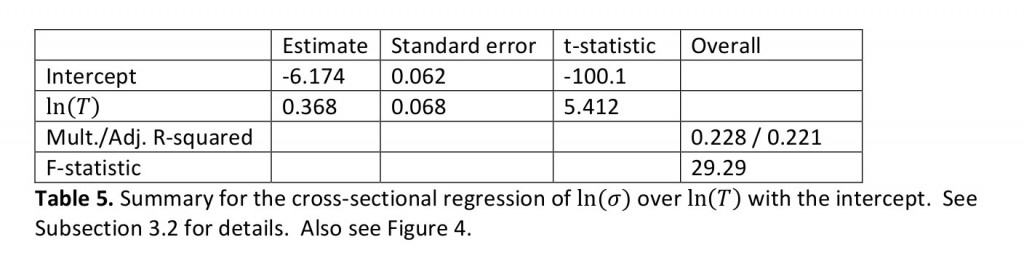
по 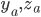 со свободным членом. Результаты представлены в таблице ниже. Очевидно, что линейная и билинейная ( в
со свободным членом. Результаты представлены в таблице ниже. Очевидно, что линейная и билинейная ( в 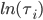 ) переменные
) переменные 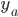 и
и 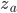 имеют низкую объясняющую силу для попарных корреляций
имеют низкую объясняющую силу для попарных корреляций 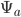 , в то время как
, в то время как 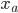 просто моделирует среднюю корреляции
просто моделирует среднюю корреляции 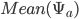 . Помните, что конструкция
. Помните, что конструкция 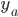 и
и 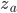 ортогональна
ортогональна 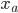 , и все три переменных независимы друг от друга.
, и все три переменных независимы друг от друга.
Подчеркнем что наше заключение не обязательно означает, что оборачиваемость не добавляет значимости в контекст факторной модели, это означает только то, что оборот как таковой не участвует в моделировании парных корреляций альфа-сигналов. Приведенный выше анализ не учитывает, добавляет ли оборачиваемость объяснительную силу для моделирования дисперсии конкретного риска. Можно обнаружить,что линейная регрессия 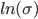 по
по 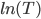 (со свободным членом) показывает ненулевое значение корреляции между этими переменными (см. таблицу ниже), хотя и не очень большое. Чтобы увидеть, добавляет ли оборот что-то к значению, например, конкретного риска, требуется использование определенных методов, что выходит за рамки данной статьи.
(со свободным членом) показывает ненулевое значение корреляции между этими переменными (см. таблицу ниже), хотя и не очень большое. Чтобы увидеть, добавляет ли оборот что-то к значению, например, конкретного риска, требуется использование определенных методов, что выходит за рамки данной статьи.
Заключение.
Отметим, что 101 сигнал, который здесь мы приводим, не “игрушечные” альфы, а те, которые реально используются в торговле. На самом деле, 80 из этих сигналов участвуют в торговле на момент написания статьи. Насколько нам известно, это первый раз, когда такое большое количество реальных формул для торговых сигналов появляется в литературе. И это неудивительно, естественно, алгоритмическая торговля является весьма секретной и скрытной. Наша цель -предоставить возможность заглянуть в сложный мир современной и постоянно развивающейся алгоритмической торговли и демистифицировать его, в какой-то степени .
Технический прогресс сегодня позволяет автоматизировать поиск альфа-сигналов. Алгоритмические альфа-сигналы, безусловно, являются самыми многочисленными доступными торговыми сигналами, которые могут быть превращены в торговые стратегии. Существует множество перестановок в отдельных ( рыночно - нейтральных) портфелях, например, из 2 000 наиболее ликвидных американских акций, которые могут обеспечить положительную доходность на высоко - и среднечастотных временных горизонтах. Кроме того, многие из этих сигналов эфемерны и их обоснования слабы. Нужно делать сложные, технологически обоснованные и постоянно адаптируемые операции для поиска сотен тысяч и миллионов торговых сигналов, чтобы потом объединить их в единый “мега-альфа” сигнал, который будет торговаться с дополнительным бонусом по доходности за счет автоматического сведения внутренних кросс- сделок.
Приложение А: Формулы альфа-сигналов.
Alpha#1: (rank(Ts_ArgMax(SignedPower(((returns < 0) ? stddev(returns, 20) : close), 2.), 5)) -0.5)
Alpha#2: (-1 * correlation(rank(delta(log(volume), 2)), rank(((close - open) / open)), 6))
Alpha#3: (-1 * correlation(rank(open), rank(volume), 10))
Alpha#4: (-1 * Ts_Rank(rank(low), 9))
Alpha#5: (rank((open - (sum(vwap, 10) / 10))) * (-1 * abs(rank((close - vwap))))) Alpha#6: (-1 * correlation(open, volume, 10))
Alpha#7: ((adv20 < volume) ? ((-1 * ts_rank(abs(delta(close, 7)), 60)) * sign(delta(close, 7))) : (-1* 1))
Alpha#8: (-1 * rank(((sum(open, 5) * sum(returns, 5)) - delay((sum(open, 5) * sum(returns, 5)),10))))
Alpha#9: ((0 < ts_min(delta(close, 1), 5)) ? delta(close, 1) : ((ts_max(delta(close, 1), 5) < 0) ?
delta(close, 1) : (-1 * delta(close, 1))))
Alpha#10: rank(((0 < ts_min(delta(close, 1), 4)) ? delta(close, 1) : ((ts_max(delta(close, 1), 4) < 0) ? delta(close, 1) : (-1 * delta(close, 1)))))
Alpha#11: ((rank(ts_max((vwap - close), 3)) + rank(ts_min((vwap - close), 3))) * rank(delta(volume, 3)))
Alpha#12: (sign(delta(volume, 1)) * (-1 * delta(close, 1)))
Alpha#13: (-1 * rank(covariance(rank(close), rank(volume), 5)))
Alpha#14: ((-1 * rank(delta(returns, 3))) * correlation(open, volume, 10))
Alpha#15: (-1 * sum(rank(correlation(rank(high), rank(volume), 3)), 3))
Alpha#16: (-1 * rank(covariance(rank(high), rank(volume), 5)))
Alpha#17: (((-1 * rank(ts_rank(close, 10))) * rank(delta(delta(close, 1), 1))) * rank(ts_rank((volume / adv20), 5)))
Alpha#18: (-1 * rank(((stddev(abs((close - open)), 5) + (close - open)) + correlation(close, open, 10))))
Alpha#19: ((-1 * sign(((close - delay(close, 7)) + delta(close, 7)))) * (1 + rank((1 + sum(returns, 250)))))
Alpha#20: (((-1 * rank((open - delay(high, 1)))) * rank((open - delay(close, 1)))) * rank((open - delay(low, 1))))
Alpha#21: ((((sum(close, 8) / 8) + stddev(close, 8)) < (sum(close, 2) / 2)) ? (-1 * 1) : (((sum(close,2) / 2) < ((sum(close, 8) / 8) - stddev(close, 8))) ? 1 : (((1 < (volume / adv20)) || ((volume /adv20) == 1)) ? 1 : (-1 * 1))))
Alpha#22: (-1 * (delta(correlation(high, volume, 5), 5) * rank(stddev(close, 20))))
Alpha#23: (((sum(high, 20) / 20) < high) ? (-1 * delta(high, 2)) : 0)
Alpha#24: ((((delta((sum(close, 100) / 100), 100) / delay(close, 100)) < 0.05) || ((delta((sum(close, 100) / 100), 100) / delay(close, 100)) == 0.05)) ? (-1 * (close - ts_min(close,100))) : (-1 * delta(close, 3)))
Alpha#25: rank(((((-1 * returns) * adv20) * vwap) * (high - close)))
Alpha#26: (-1 * ts_max(correlation(ts_rank(volume, 5), ts_rank(high, 5), 5), 3))
Alpha#27: ((0.5 < rank((sum(correlation(rank(volume), rank(vwap), 6), 2) / 2.0))) ? (-1 * 1) : 1) Alpha#28: scale(((correlation(adv20, low, 5) + ((high + low) /2)) - close))
Alpha#29: (min(product(rank(rank(scale(log(sum(ts_min(rank(rank((-1 * rank(delta((close - 1), 5))))), 2), 1))))), 1), 5) + ts_rank(delay((-1 * returns), 6), 5))
Alpha#30: (((1.0 - rank(((sign((close - delay(close, 1))) + sign((delay(close, 1) - delay(close, 2)))) +sign((delay(close, 2) - delay(close, 3)))))) * sum(volume, 5)) / sum(volume, 20))
Alpha#31: ((rank(rank(rank(decay_linear((-1 * rank(rank(delta(close, 10)))), 10)))) + rank((-1 * delta(close, 3)))) + sign(scale(correlation(adv20, low, 12))))
Alpha#32: (scale(((sum(close, 7) / 7) - close)) + (20 * scale(correlation(vwap, delay(close, 5),230))))
Alpha#33: rank((-1 * ((1 - (open / close))^1)))
Alpha#34: rank(((1 - rank((stddev(returns, 2) / stddev(returns, 5)))) + (1 - rank(delta(close, 1)))))
Alpha#35: ((Ts_Rank(volume, 32) * (1 - Ts_Rank(((close + high) - low), 16))) * (1 - Ts_Rank(returns, 32)))
Alpha#36: (((((2.21 * rank(correlation((close - open), delay(volume, 1), 15))) + (0.7 * rank((open- close)))) + (0.73 * rank(Ts_Rank(delay((-1 * returns), 6), 5)))) + rank(abs(correlation(vwap, adv20, 6)))) + (0.6 * rank((((sum(close, 200) / 200) - open) * (close - open)))))
Alpha#37: (rank(correlation(delay((open - close), 1), close, 200)) + rank((open - close))) Alpha#38: ((-1 * rank(Ts_Rank(close, 10))) * rank((close / open)))
Alpha#39: ((-1 * rank((delta(close, 7) * (1 - rank(decay_linear((volume / adv20), 9)))))) * (1 +rank(sum(returns, 250))))
Alpha#40: ((-1 * rank(stddev(high, 10))) * correlation(high, volume, 10)) Alpha#41: (((high * low)^0.5) - vwap)
Alpha#42: (rank((vwap - close)) / rank((vwap + close)))
Alpha#43: (ts_rank((volume / adv20), 20) * ts_rank((-1 * delta(close, 7)), 8))
Alpha#44: (-1 * correlation(high, rank(volume), 5))
Alpha#45: (-1 * ((rank((sum(delay(close, 5), 20) / 20)) * correlation(close, volume, 2)) *rank(correlation(sum(close, 5), sum(close, 20), 2))))
Alpha#46: ((0.25 < (((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10))) ?(-1 * 1) : (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < 0) ? 1 :((-1 * 1) * (close - delay(close, 1)))))
Alpha#47: ((((rank((1 / close)) * volume) / adv20) * ((high * rank((high - close))) / (sum(high, 5) / 5))) - rank((vwap - delay(vwap, 5))))
Alpha#48: (indneutralize(((correlation(delta(close, 1), delta(delay(close, 1), 1), 250) * delta(close, 1)) / close), IndClass.subindustry) / sum(((delta(close, 1) / delay(close, 1))^2), 250))
Alpha#49: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.1)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#50: (-1 * ts_max(rank(correlation(rank(volume), rank(vwap), 5)), 5))
Alpha#51: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.05)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#52: ((((-1 * ts_min(low, 5)) + delay(ts_min(low, 5), 5)) * rank(((sum(returns, 240) -sum(returns, 20)) / 220))) * ts_rank(volume, 5))
Alpha#53: (-1 * delta((((close - low) - (high - close)) / (close - low)), 9))
Alpha#54: ((-1 * ((low - close) * (open^5))) / ((low - high) * (close^5)))
Alpha#55: (-1 * correlation(rank(((close - ts_min(low, 12)) / (ts_max(high, 12) - ts_min(low, 12)))), rank(volume), 6))
Alpha#56: (0 - (1 * (rank((sum(returns, 10) / sum(sum(returns, 2), 3))) * rank((returns * cap)))))
Alpha#57: (0 - (1 * ((close - vwap) / decay_linear(rank(ts_argmax(close, 30)), 2))))
Alpha#58: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.sector), volume, 3.92795), 7.89291), 5.50322))
Alpha#59: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(((vwap * 0.728317) + (vwap * (1 - 0.728317))), IndClass.industry), volume, 4.25197),
16.2289), 8.19648))
Alpha#60: (0 - (1 * ((2 * scale(rank(((((close - low) - (high - close)) / (high - low)) * volume)))) - scale(rank(ts_argmax(close, 10))))))
Alpha#61: (rank((vwap - ts_min(vwap, 16.1219))) < rank(correlation(vwap, adv180, 17.9282)))
Alpha#62: ((rank(correlation(vwap, sum(adv20, 22.4101), 9.91009)) < rank(((rank(open) + rank(open)) < (rank(((high + low) / 2)) + rank(high))))) * -1)
Alpha#63: ((rank(decay_linear(delta(IndNeutralize(close, IndClass.industry), 2.25164), 8.22237))- rank(decay_linear(correlation(((vwap * 0.318108) + (open * (1 - 0.318108))), sum(adv180, 37.2467), 13.557), 12.2883))) * -1)
Alpha#64: ((rank(correlation(sum(((open * 0.178404) + (low * (1 - 0.178404))), 12.7054),sum(adv120, 12.7054), 16.6208)) < rank(delta(((((high + low) / 2) * 0.178404) + (vwap * (1 -0.178404))), 3.69741))) * -1)
Alpha#65: ((rank(correlation(((open * 0.00817205) + (vwap * (1 - 0.00817205))), sum(adv60, 8.6911), 6.40374)) < rank((open - ts_min(open, 13.635)))) * -1)
Alpha#66: ((rank(decay_linear(delta(vwap, 3.51013), 7.23052)) + Ts_Rank(decay_linear(((((low* 0.96633) + (low * (1 - 0.96633))) - vwap) / (open - ((high + low) / 2))), 11.4157), 6.72611)) * -1)
Alpha#67: ((rank((high - ts_min(high, 2.14593)))^rank(correlation(IndNeutralize(vwap, IndClass.sector), IndNeutralize(adv20, IndClass.subindustry), 6.02936))) * -1)
Alpha#68: ((Ts_Rank(correlation(rank(high), rank(adv15), 8.91644), 13.9333) <rank(delta(((close * 0.518371) + (low * (1 - 0.518371))), 1.06157))) * -1)
Alpha#69: ((rank(ts_max(delta(IndNeutralize(vwap, IndClass.industry), 2.72412), 4.79344))^Ts_Rank(correlation(((close * 0.490655) + (vwap * (1 - 0.490655))), adv20, 4.92416),9.0615)) * -1)
Alpha#70: ((rank(delta(vwap, 1.29456))^Ts_Rank(correlation(IndNeutralize(close, IndClass.industry), adv50, 17.8256), 17.9171)) * -1)
Alpha#71: max(Ts_Rank(decay_linear(correlation(Ts_Rank(close, 3.43976), Ts_Rank(adv180, 12.0647), 18.0175), 4.20501), 15.6948), Ts_Rank(decay_linear((rank(((low + open) - (vwap +vwap)))^2), 16.4662), 4.4388))
Alpha#72: (rank(decay_linear(correlation(((high + low) / 2), adv40, 8.93345), 10.1519)) / rank(decay_linear(correlation(Ts_Rank(vwap, 3.72469), Ts_Rank(volume, 18.5188), 6.86671),2.95011)))
Alpha#73: (max(rank(decay_linear(delta(vwap, 4.72775), 2.91864)),Ts_Rank(decay_linear(((delta(((open * 0.147155) + (low * (1 - 0.147155))), 2.03608) / ((open *0.147155) + (low * (1 - 0.147155)))) * -1), 3.33829), 16.7411)) * -1)
Alpha#74: ((rank(correlation(close, sum(adv30, 37.4843), 15.1365)) <rank(correlation(rank(((high * 0.0261661) + (vwap * (1 - 0.0261661)))), rank(volume), 11.4791)))* -1)
Alpha#75: (rank(correlation(vwap, volume, 4.24304)) < rank(correlation(rank(low), rank(adv50), 12.4413)))
Alpha#76: (max(rank(decay_linear(delta(vwap, 1.24383), 11.8259)), Ts_Rank(decay_linear(Ts_Rank(correlation(IndNeutralize(low, IndClass.sector), adv81, 8.14941), 19.569), 17.1543), 19.383)) * -1)
Alpha#77: min(rank(decay_linear(((((high + low) / 2) + high) - (vwap + high)), 20.0451)), rank(decay_linear(correlation(((high + low) / 2), adv40, 3.1614), 5.64125)))
Alpha#78: (rank(correlation(sum(((low * 0.352233) + (vwap * (1 - 0.352233))), 19.7428),sum(adv40, 19.7428), 6.83313))^rank(correlation(rank(vwap), rank(volume), 5.77492)))
Alpha#79: (rank(delta(IndNeutralize(((close * 0.60733) + (open * (1 - 0.60733))), IndClass.sector), 1.23438)) < rank(correlation(Ts_Rank(vwap, 3.60973), Ts_Rank(adv150,9.18637), 14.6644)))
Alpha#80: ((rank(Sign(delta(IndNeutralize(((open * 0.868128) + (high * (1 - 0.868128))), IndClass.industry), 4.04545)))^Ts_Rank(correlation(high, adv10, 5.11456), 5.53756)) * -1)
Alpha#81: ((rank(Log(product(rank((rank(correlation(vwap, sum(adv10, 49.6054), 8.47743))^4)), 14.9655))) < rank(correlation(rank(vwap), rank(volume), 5.07914))) * -1)
Alpha#82: (min(rank(decay_linear(delta(open, 1.46063), 14.8717)), Ts_Rank(decay_linear(correlation(IndNeutralize(volume, IndClass.sector), ((open * 0.634196) + (open * (1 - 0.634196))), 17.4842), 6.92131), 13.4283)) * -1)
Alpha#83: ((rank(delay(((high - low) / (sum(close, 5) / 5)), 2)) * rank(rank(volume))) / (((high - low) / (sum(close, 5) / 5)) / (vwap - close)))
Alpha#84: SignedPower(Ts_Rank((vwap - ts_max(vwap, 15.3217)), 20.7127), delta(close, 4.96796))
Alpha#85: (rank(correlation(((high * 0.876703) + (close * (1 - 0.876703))), adv30, 9.61331))^rank(correlation(Ts_Rank(((high + low) / 2), 3.70596), Ts_Rank(volume, 10.1595),7.11408)))
Alpha#86: ((Ts_Rank(correlation(close, sum(adv20, 14.7444), 6.00049), 20.4195) < rank(((open+ close) - (vwap + open)))) * -1)
Alpha#87: (max(rank(decay_linear(delta(((close * 0.369701) + (vwap * (1 - 0.369701))), 1.91233), 2.65461)), Ts_Rank(decay_linear(abs(correlation(IndNeutralize(adv81,IndClass.industry), close, 13.4132)), 4.89768), 14.4535)) * -1)
Alpha#88: min(rank(decay_linear(((rank(open) + rank(low)) - (rank(high) + rank(close))), 8.06882)), Ts_Rank(decay_linear(correlation(Ts_Rank(close, 8.44728), Ts_Rank(adv60,20.6966), 8.01266), 6.65053), 2.61957))
Alpha#89: (Ts_Rank(decay_linear(correlation(((low * 0.967285) + (low * (1 - 0.967285))), adv10, 6.94279), 5.51607), 3.79744) - Ts_Rank(decay_linear(delta(IndNeutralize(vwap,IndClass.industry), 3.48158), 10.1466), 15.3012))
Alpha#90: ((rank((close - ts_max(close, 4.66719)))^Ts_Rank(correlation(IndNeutralize(adv40, IndClass.subindustry), low, 5.38375), 3.21856)) * -1)
Alpha#91: ((Ts_Rank(decay_linear(decay_linear(correlation(IndNeutralize(close, IndClass.industry), volume, 9.74928), 16.398), 3.83219), 4.8667) -
rank(decay_linear(correlation(vwap, adv30, 4.01303), 2.6809))) * -1)
Alpha#92: min(Ts_Rank(decay_linear(((((high + low) / 2) + close) < (low + open)), 14.7221), 18.8683), Ts_Rank(decay_linear(correlation(rank(low), rank(adv30), 7.58555), 6.94024),6.80584))
Alpha#93: (Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.industry), adv81, 17.4193), 19.848), 7.54455) / rank(decay_linear(delta(((close * 0.524434) + (vwap * (1 -0.524434))), 2.77377), 16.2664)))
Alpha#94: ((rank((vwap - ts_min(vwap, 11.5783)))^Ts_Rank(correlation(Ts_Rank(vwap, 19.6462), Ts_Rank(adv60, 4.02992), 18.0926), 2.70756)) * -1)
Alpha#95: (rank((open - ts_min(open, 12.4105))) < Ts_Rank((rank(correlation(sum(((high + low)/ 2), 19.1351), sum(adv40, 19.1351), 12.8742))^5), 11.7584))
Alpha#96: (max(Ts_Rank(decay_linear(correlation(rank(vwap), rank(volume), 3.83878), 4.16783), 8.38151), Ts_Rank(decay_linear(Ts_ArgMax(correlation(Ts_Rank(close, 7.45404),Ts_Rank(adv60, 4.13242), 3.65459), 12.6556), 14.0365), 13.4143)) * -1)
Alpha#97: ((rank(decay_linear(delta(IndNeutralize(((low * 0.721001) + (vwap * (1 - 0.721001))), IndClass.industry), 3.3705), 20.4523)) - Ts_Rank(decay_linear(Ts_Rank(correlation(Ts_Rank(low,7.87871), Ts_Rank(adv60, 17.255), 4.97547), 18.5925), 15.7152), 6.71659)) * -1)
Alpha#98: (rank(decay_linear(correlation(vwap, sum(adv5, 26.4719), 4.58418), 7.18088)) -rank(decay_linear(Ts_Rank(Ts_ArgMin(correlation(rank(open), rank(adv15), 20.8187), 8.62571),6.95668), 8.07206)))
Alpha#99: ((rank(correlation(sum(((high + low) / 2), 19.8975), sum(adv60, 19.8975), 8.8136)) <rank(correlation(low, volume, 6.28259))) * -1)
Alpha#100: (0 - (1 * (((1.5 * scale(indneutralize(indneutralize(rank(((((close - low) - (high - close)) / (high - low)) * volume)), IndClass.subindustry), IndClass.subindustry))) - scale(indneutralize((correlation(close, rank(adv20), 5) - rank(ts_argmin(close, 30))), IndClass.subindustry))) * (volume / adv20))))
Alpha#101: ((close - open) / ((high - low) + .001))
А1. Функции и операторы
abs(x), log(x), sign(x) = стандартные определения функций; то же для операторов “+”, “-”, “*”, “/”, “>”, “<”, “==”, “||”, “x ? y : z”
rank(x) = кросс-секционный ранг
delay(x, d) = значение x d дней назад
correlation(x, y, d) = корреляция временных серий x и y за последние d дней
covariance(x, y, d) =ковариация временных серий x и y за последние d дней
scale(x, a) = масштабирование x таким образом,что sum(abs(x)) = a ( начальное значение a = 1)
delta(x, d) = сегодняшнее значение x минус значение x d дней назад
signedpower(x, a) = x^a
decay_linear(x, d) = взвешенная скользящая средняя за последние d дней с линейно снижающимися весами d, d – 1, …, 1 (сумма весов должна быть равна 1)
indneutralize(x, g) = x кросс-секционально нейтрализовано к группе g (субиндустрия, индустрия, секторы, и т.д.), то есть, x кросс-секционно не влиеяет на группу g
ts_{O}(x, d) = оператор O применен к временной серии за последние d дней; нецелое число дней d преобразуется к floor(d)
ts_min(x, d) = минимум временной серии за последние d дней
ts_max(x, d) =макисмум временной серии за последние d дней
ts_argmax(x, d) = в какой день происходит ts_max(x, d)
ts_argmin(x, d) =в какой день происходит ts_min(x, d)
ts_rank(x, d) = ранг временной серии за последние d дней
min(x, d) = ts_min(x, d)
max(x, d) = ts_max(x, d)
sum(x, d) = сумма временной серии за последние d дней
product(x, d) = произведение временной серии за последние d дней
stddev(x, d) = скользящее среднеквадратичное отклонение временной серии за последние d дней
А2. Входные данные
returns = дневное приращение цены от закрытия к закрытию
open, close, high, low, volume = стандартные определения для дневных цен и объемов
vwap = дневная взвешенная по объему цена
cap = рыночная капитализация
adv{d} = средний денежный объем за последние d дней
IndClass = основное определение для бинарной индустриальной классификации (ОКВЭД и т.п.) в indneutralize(x, IndClass.level), где level = сектор, индустрия, субиндустрия и т.д.
Множественные IndClass в одном и том же сигнале не относятся к одинаковой классификации по индустриям.



Из статьи не понял кое что.
"ts_rank(x, d) = ранг временной серии за последние d дней"
Это позиция последнего значения серии, в отсортированном списке всех значений серии?
Может кто-то пояснить, что такое "кросс-секционный ранг"?
Нет, все понятно, но шо конкретно? 🙂
Спасибо.
Кросс-секционный ранг - это ранг ковариационной матрицы. Что такое ранг матрицы, можете найти здесь - https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%BD%D0%B3_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B
Берут меня сомнения.
"rank(x) = кросс-секционный ранг"
для ковариационной матрицы нужно задать размерность, в нашем случае это длина серии. В ts_rank(x, d) длина серии есть, а в rank(x) нет.
Не понятно.
Еще одна версия.
кросс-секционный ранг - это номер позиции, в отсортированном по некоторому критерию, списке активов (акции, ETF и т.д).
Т.е. например берем список из SP500 и сортируем акции по дневной доходности. номер нашей акции и есть ранг.
Что думаете коллеги?
Я тоже так понял эту функцию. То есть, по-русски, ранжирование ряда. Просто rank ранжирует по всему ряду, ts_rank ранжирует в окне. Вот только непонятно что такое "кросс-секционный".
<code>
> x
[1] 4 5 6 8 8 9 5 6 2 8 20
> rank(x)
[1] 2.0 3.5 5.5 8.0 8.0 10.0 3.5 5.5 1.0 8.0 11.0
> ts_rank(x,3)
[1] 3.0 3.0 2.5 3.0 1.0 2.0 1.0 3.0 3.0
</code>
А как определить, какой из сигналов является реверсивным, а какой - импульсным? И что вообще означает полученный результат?