QuantAlgos

Продолжение. Начало здесь.

Модель, устойчивая к смене режимов волатильности

Некоторые проблемы торговли спредом

Ранее мы определили три сосотавляющих рыночно-нейтральных стратегий. Здесь мы обновим эту классификацию и рассмотрим некоторые трудности, связвнные с торговлей спредом.

Долговременные расхождения в ценах трудно найти с помощью алгоритмов, основанных только на ценах. Обычно, фундаментальный анализ, совместно с опытом трейдера может помочь в понимании существования  расхождения. Время возврата к среднему может быть установлено с помощью непрерывных моделей, в этом случае период удержания позиции зависит от модели спреда и, следовательно, от частоты пересчета коэффициента хэджирования.

Много факторов могут приводить к скачкам волатильности спреда, но сами по себе скачки не могут быть приняты в качестве сигналов прекращения торговли парой.

При частом обновлении коэффициента хэджирования предпочтительней определять скачки в волатильности, чем в среднем значении. С другой стороны, если коэффициент меняется не так часто, переходы среднего значения также можно вычислять, так как спред начинает демонстрировать сильную зависимость от будущего отношения цен.

Стратегия тестирования из трех частей

1. Идентификация пары

В этой части мы применим некоторые понятия, представленные выше, в качестве фильтра включения/исключения актива для нашего алгоритма. Так как мы используем внутридневные данные, фильтры вычисляются с дневной частотой, то есть длина тренировочного и тестового набора состоят из 11 часов предыдущего дня.

Семь пар было выбрано с целью избежать ложной корреляции или случайных совпадений. Так как мы тестируем стратегии на сырьевых и индексных фьючерсах, мы не фокусируемся на фундаментальном анализе, он мог бы рекомендоваться при торговле акциями.

Мы применим три простых фильтра:

• 5% -й уровень значимости коэффициента наклона линейной регрессии;
• корреляция между ценами более более 80%;
• 5% уровень значимости коинтеграционного отношения между ценами двух активов, по статье D. Kwiatkowski, P. C. B. Phillips, P. Schmidt, and Y. Shin. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54:159–178, 1992.

2. Моделирование спреда

Спред определяется как взвешенная разность между двумя ценами:

$spread=P_{1t}-\beta P_{2t}$

Частота выборки равна 10 или 20 минутам, и коэффициент хэджирования $\beta$ обновляется каждый день, используя данные предыдущего дня, путем метода усреднения коэффициента минимальной дисперсии (смотрите обзор литературы в предыдущей части). Частота обновления соответствует строго внутридневной модели торговли.

Этот выбор имеет преимущество в связи с избежанием начисления ночной маржи на открытую позицию, в то же время, позиция не удерживается более одного торгового дня, что является довольно жестким ограничением.

3. Торговый алгоритм

Торговая модель представляет собой обычную стратегию с возвратом к среднему, использующую диапазоны Боллинджера.Эта модель применяет четыре диапазона, самы широкий в качестве сигнала входа, а самый узкий - как сигнал выхода из позиции. Как следствие, стратегия не все время находится в рынке. Есть только один дополнительный сигнал выхода ( не являющийся взятием прибыли), соответствующий окончанию торгового дня.

Эта стратегия сравнивается с другой, которая использует порог волатильности для определения коэффициента при дисперсии (ширины полос Боллинджера) , лучше подходящий текущему состоянию волатильности. Таким образом, существует восемь диапазонов, четыре для низкой волатильности и четыре - для высокой.

В качестве примера первая модель ( с 4 диапазонами) показана на рисунке ниже. Когда закрытие свечи выше сплошной линии, мы продаем актив, и наоборот, когда цена закрытия уходит под нижнию линию. Для узкого диапазона, соответственно, верхняя линия - выход из длинной позиции, а нижняя - выход из короткой. Так как мы ожидаем контртрендовое поведение спреда, то делаем ставку на внутридневной возврат к среднему.

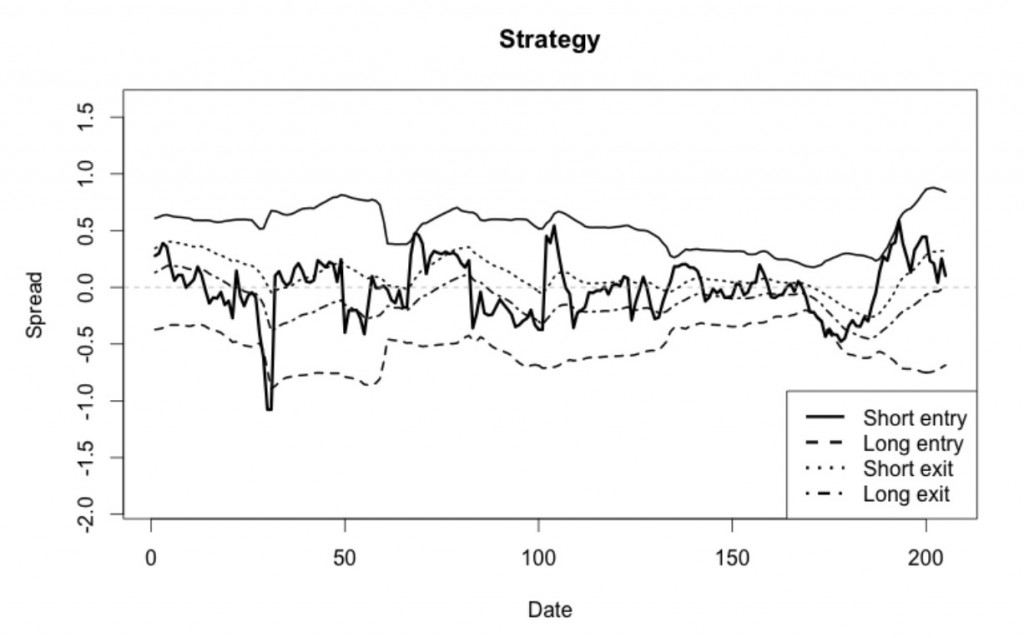Следующая  система основана на двух разных режимах. Инидикаторы разделены на три группы: уровни входа, уровни выхода и порог переключения режимов. Порог является различием между первой моделью и нашим подходом, и гауссовская смесь и НММ играют ключевую роль в его определении.

Так как порог указывает на уровень волатильности, соответствующий переходу от одного режима к другому, задача состоит в их правильном определении. Для гауссовской смеси мы используем, как порог, большее стандартное отклонение из двух, составляющих смесь, популяций. Также, для НММ мы применяем большее стандартное отклонение из двух моделей перехода.

Результаты

Мы разделили данные на четыре выборки, использовав первую и третью как тренировочные наборы. Также, мы установили порог равным средним значениям двух тренировочных наборов. Затем мы применили эти величины для тестирования стратегии с единым порогом для всех выборок.

Все вычисления производились на языке R. Конкретно, использовались библиотеки mixtools и MSwM, соответственно, для гауссовской смеси и модели Маркова. В обоих случаях максимальное правдободобие находилось с помощью ЕМ алгоритма. Так как размер выборки был приблизительно равен 4500, время вычислений достаточно мало, несколько секунд в случае гауссовской смеси и около минуты для НММ.

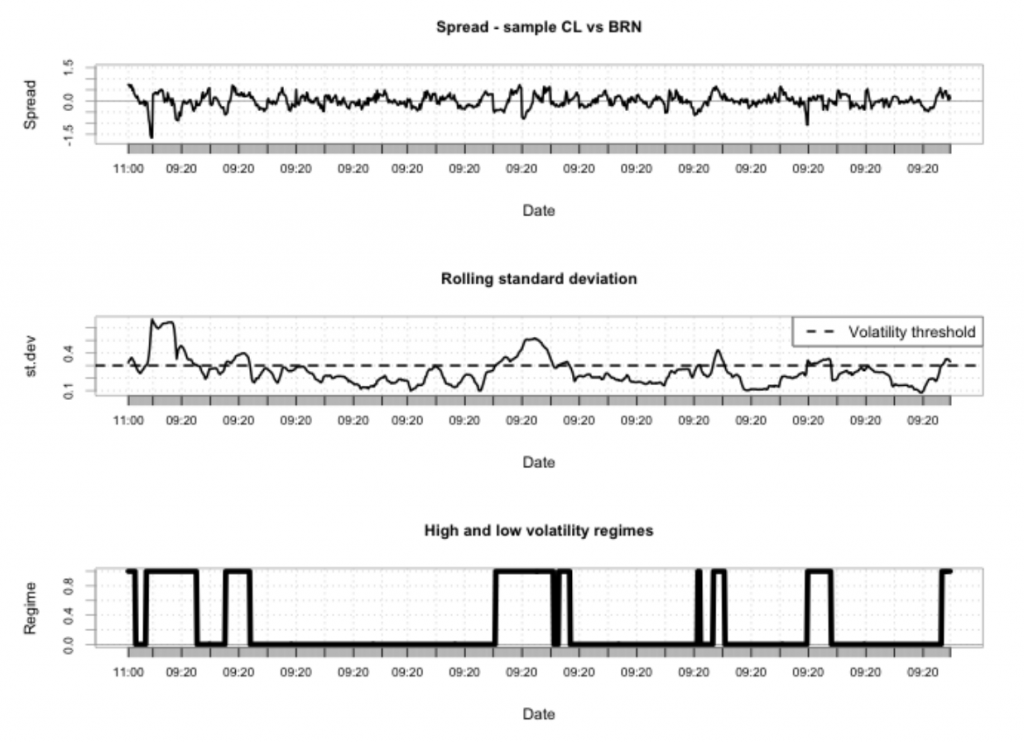
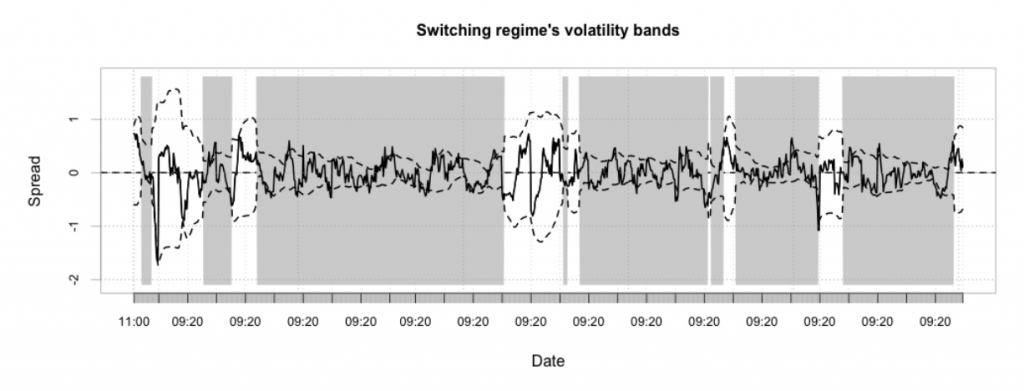
Три области на рисунке в заглавии статьи графически представляют, как определялись режимы. Верхняя панель показывает, что периоды высокой волатильности сменялись периодами низкой волатильности и такое поведение носило перманентный характер. Средняя панель показывает скользящее стандартное отклонение с порогом (прерывистая линия): режимы высокой волатильности соответствуют периодам, где стандартное отклонение выше линии, низковолатильные режимы соответствуют обратной ситуации. Нижняя панель отражает сами режимы. На рисунке ниже показано, как уровни входа изменяются соответственно с определенной волатильностью. Отметим, что выходы меняются подобным же образом.

В следующей части мы продолжим разбор результатов тестирования и сделаем соответствующие выводы.