В статьях об индикаторе PIN мы определили, что на рынке присутствуют два типа трейдеров - информированные и неинформированные. Заявки неинформированных трейдеров всегда подвержены adverse selection risk со стороны информированных. Ситуация, когда после исполнения таких заявок цена движется в невыгодную для неинформированных участников сторону, называется токсичностью потока ордеров. Индикатор PIN служил для измерения этой токсичности, в данной статье мы рассмотрим усовершенствованный индикатор VPIN, который применим и для высокочастотной торговли. Цикл статей основан на публикации Maureen O’Hara "Flow Toxicity and Liquidity in a High Frequency World". Будет все описываться очень подробно, потому что, кроме нахождения непосредственно VPIN, в этой публикации много интересных выводов и фактов.
Из фундаментальных исследований о микроструктуре рынка известно, что процесс поступления ордеров информативен в отношении последующего движения цены в общем случае, и токсичности потока в частности. Извлечение этой информации, однако, затруднено из-за сложной природы высокочастотных рынков. Мы утверждаем, что в высокочастотной области привязка к сделкам более релевантна, чем привязка к текущему времени. Мы применим наши исследования к рынку фьючерсов, где информация более связана с систематическими факторами, отражающими процессы хеджирования или портфельной диверсификации.
Мы представим новую процедуру оценки токсичности потока заявок прямо и аналитически, основанную на процессе, зависимом от поступающих объемов , который назовем "синхронизированная по объемам вероятность информированной торговли" (Volume-Synchronized Probability of Informed Trading), или VPIN. Подход, основанный на VPIN, не требует промежуточной числовой оценки ненаблюдаемых параметров, как в случае с PIN, и обновляется в стохастическом времени, которое откалибровано по одинаковому объему сделок в каждый его промежуток. Таким образом, наша модель избегает трудности вычисления индикатора PIN на высокоактивных рынках и предоставляет аналитический способ измерять токсичность потока ордеров при использовании высокочастотных исходных данных.
Мы определим эмпирически статистические свойства VPIN и покажем, как объемное пакетирование ( таким образом, что каждый выбранный интервал времени содержит одинаковый объем сделок) снижает скачки волатильности (кластерность) в выборке. Так как большие движения цены ассоциируются с большими объемами, выборка по объемам является отражением выборки по волатильности. Результирующая временная серия наблюдений следует статистическому распределению, которое близко к нормальному и менее гетероскедастична, чем серии с одинаковыми временными интервалами (см. график в заглавии поста).
Применение и полезность VPIN будут демонстрироваться на фьючерсах E-mini S&P500 и фьючерсных контрактах на сырую нефть WTI . Также мы покажем, что VPIN имеет важную связь с будущей изменчивостью цены. Так как токсичность опасна для провайдеров ликвидности (маркет-мейкеров), высокие значения VPIN должны предупреждать о высокой волатильности. Мы увидим, что VPIN предсказывает краткосрочную, вызванную токсичностью, волатильность, частично связанную с большими движениями цены.
Оценка токсичности потока ордеров имеет множество практических применений. Маркет-мейкеры могут использовать VPIN в качестве инструмента управления риском в реальном масштабе времени. Применение VPIN трейдерами может ограничить успешность алгоритмов-хищников, получающих прибыль от атаки на провайдеров ликвидности. Также можно использовать VPIN для создания алгоритмов управления риском исполнения (execution control).
Модель
Микроструктурную модель рынка можно представить в виде игры между провайдерами ликвидности и трейдерами (потребителями ликвидности), которая повторяется на периодах i=1,...,I. В начале каждого периода возникает какое-либо информационное событие. События возникают независимо с вероятностью  . Если это хорошие новости, то информированный трейдер знает, что в конце периода цена достигнет уровня
. Если это хорошие новости, то информированный трейдер знает, что в конце периода цена достигнет уровня 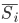 , а если плохие, то уровня
, а если плохие, то уровня 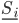 , где
, где 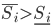 . Хорошие новости возникают с вероятностью
. Хорошие новости возникают с вероятностью 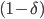 , и плохие, соответственно, с вероятностью
, и плохие, соответственно, с вероятностью 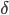 . После того, как событие возникнет, или не возникнет, торговля в этот период начинается с прибытия трейдеров в соответствии с Пуассоновским процессом и далее в течение всего периода. В периоды с возникшим информационным событием заявки от информированных трейдеров поступают с частотой
. После того, как событие возникнет, или не возникнет, торговля в этот период начинается с прибытия трейдеров в соответствии с Пуассоновским процессом и далее в течение всего периода. В периоды с возникшим информационным событием заявки от информированных трейдеров поступают с частотой 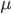 . Эти трейдеры покупают при хороших новостях и продают при плохих. В каждом периоде ордера на покупку и продажу от неинформированных трейдеров поступают с частотой
. Эти трейдеры покупают при хороших новостях и продают при плохих. В каждом периоде ордера на покупку и продажу от неинформированных трейдеров поступают с частотой 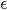 для каждого вида заявки. Повышенные объемы покупки или продажи трактуются как торговля на основе информации и применяются для идентификации
для каждого вида заявки. Повышенные объемы покупки или продажи трактуются как торговля на основе информации и применяются для идентификации 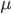 . Число периодов, где зафиксирована повышенная активность, используются для идентификации
. Число периодов, где зафиксирована повышенная активность, используются для идентификации  и
и 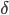 .
.
Провайдер ликвидности использует свои знания об этих параметрах для определения цены, по которой он хочет войти в длинную позицию, Bid, и цену, по которой войдет в короткую, Ask. Эти цены различны и формируют Bid-Ask Spread, так как маркетмейкер не знает, информирован его контрагент в сделке, или нет. Спред представляет собой разницу между ожидаемым значением актива при условии, что кто-то хочет купить его у провайдера ликвидности и ожидаемым значением актива при условии, что кто-то хочет продать его провайдеру на этом уровне. Эти условные ожидания различны по причине проблемы adverse selection, вызываемой возможным присутствием информированных трейдеров.
Провайдер ликвидности наблюдает за происходящими сделками и моделирует их так, если бы они следовали правилу Байеса, для обновления своих ожиданий о токсичности потока ордеров, который в нашей модели выражается через установленные параметры.Обозначим 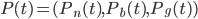 ожидания провайдера о событиях "нет новостей" (n), "плохие новости" (b) и "хорошие новости" (g) в момент времени t. В момент времени 0 он ожидает
ожидания провайдера о событиях "нет новостей" (n), "плохие новости" (b) и "хорошие новости" (g) в момент времени t. В момент времени 0 он ожидает 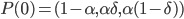 .
.
Для определения Bid и Ask в момент времени t , провайдер ликвидности обновляет свои ожидания в зависимости от прибытия ордера соответствующего типа. В момент времени t ожидаемое значение актива при условии произошедшей сделки до времени t равно:
![E[S_i|t]=P_n(t)S_i^*+P_b(t)\underline{S_i}+P_g(t)\bar{S_i}](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_a9791f07d0a89b6c7ea92fbcea3529f6.gif)
где 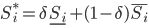 - предыдущее ожидаемое значение цены актива.
- предыдущее ожидаемое значение цены актива.
Bid в таком случае равен:
![B(t)=E[S_i|t]-\frac{\mu P_b(t)}{\epsilon+\mu P_b(t)}(E[S_i|t]-\underline{S_i})](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_ad8be74c309d2e736fc0fc080178b015.gif)
Аналогично, выражение для Ask:
![A(t)=E[S_i|t]+\frac{\mu P_g(t)}{\epsilon+\mu P_g(t)}(\bar{S_i}-E[S_i|t])](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_fb831eba294a5e0c048c2c92b6d0df1e.gif)
Эти выражения показывают отдельные роли, которые играют прибывающие ордера от информированных и неинформированных трейдеров в отношении их влияния на цену актива. Если информированные участники отсутствуют (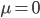 ), то сделки не несут информации и таким образом Bid и Ask равны предыдущему значению цены. В другом случае, если нет неинформированных трейдеров (
), то сделки не несут информации и таким образом Bid и Ask равны предыдущему значению цены. В другом случае, если нет неинформированных трейдеров (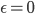 ), тогда Bid и Ask равны минимальной и макимальной ценам соответственно. По этим ценам информированные трейдеры торговать не будут и торговля прекратится. В общем случае, и те и другие участники присутствуют на рынке, и тогда Bid меньше , а Ask больше, чем
), тогда Bid и Ask равны минимальной и макимальной ценам соответственно. По этим ценам информированные трейдеры торговать не будут и торговля прекратится. В общем случае, и те и другие участники присутствуют на рынке, и тогда Bid меньше , а Ask больше, чем ![E[S_i|t]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_374b2fa375dc28e78194349c85507f99.gif) .
.
Спред между Bid и Ask в момент времени t обозначим 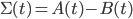 . Тогда получим:
. Тогда получим:
![\Sigma(t)=\frac{\mu P_g(t)}{\epsilon+\mu P_g(t)}(\bar{S_i}-E[S_i|t])+\frac{\mu P_b(t)}{\epsilon+\mu P_b(t)}(E[S_i|t]-\underline{S_i})](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_b9439a7add04f30d4a169e6715f7d70a.gif)
Ключевой компонент модели это вероятность того, что ордер поступил от информированного трейдера, называемая PIN. Эту вероятность можно вычислить следующим образом (см. статьи о PIN):
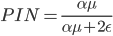
где 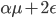 - частота поступления всех ордеров и
- частота поступления всех ордеров и 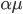 - частота ордеров информированных трейдеров. PIN, таким образом, мера отношения ордеров информированных трейдеров к общему потоку ордеров и выражение для спреда показывает, что это ключевой показатель для определения спреда.
- частота ордеров информированных трейдеров. PIN, таким образом, мера отношения ордеров информированных трейдеров к общему потоку ордеров и выражение для спреда показывает, что это ключевой показатель для определения спреда.
Эти формулы демонстрируют идею, что провайдеры ликвидности должны правильно оценивать PIN для определения оптимальных уровней, на которых они входят в рынок. Значительные изменения PIN приводят к потерям тех маркет-мейкеров, которые не корректируют свои цены в соответствии с этим показателем.
В следующей части мы перейдем к определению VPIN, усовершенствованной и легче вычисляемой метрикой по сравнению с PIN, и найдем все его параметры.

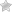


Пакет для R для таких вычислений https://cran.r-project.org/web/packages/FinAsym/index.html